b-tree 개념과 삽입, 삭제 알아보기

😮 M원 검색 트리(M-way Search Tree)

B 트리 이전에 먼저 M원 검색 트리를 알아야 한다.

• 이진 탐색 트리(BST)의 차수는 2이기 때문에 높이가 높아지는 단점이 있다.
• M원 검색 트리는 차수를 2에서 m개로 늘려 높이를 낮춘 것이다.

[특징]

• 각 노드는 m-1 개의 레코드와 m개의 서브트리를 가질 수 있다.
• 이진 탐색 트리의 확장된 형태로 높이를 줄일 수 있다.
• 각 노드 안에서는 정렬되어 있다.

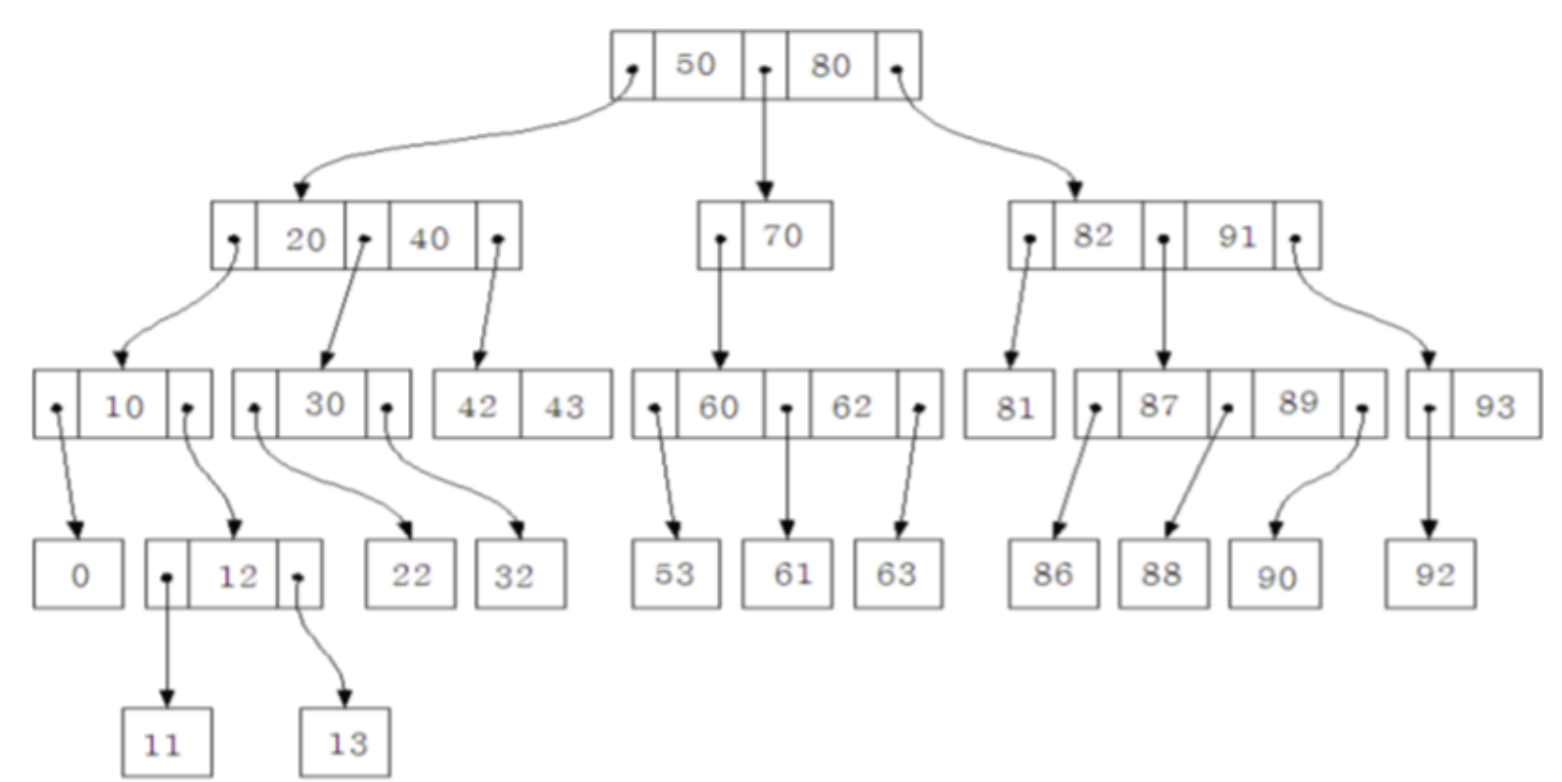
[3원 검색 트리 예시]

• 각 노드에는 2개의 레코드를 가질 수 있고 3개의 서브트리를 가질 수 있다.
• 높이가 3인 3원 검색 트리는 최대 54개의 원소를 저장할 수 있지만, 높이가 3인 BST는 최대 31개 밖에 저장하지 못한다.

🤔 B 트리(B-Tree)

• 데이터베이스, 파일 시스템에서 널리 사용되는 트리 자료구조의 일종이다.
• 단순하고 효율적이며, 레벨로만 따지면 완전히 균형을 맞춘 트리이다.
• M원 검색 트리로 높이를 줄일 수 있지만 균형이 맞지 않는다는 문제가 있다.
  • 따라서 B트리는 아래와 같은 특징으로 균형을 유지한다.

[특징]

• M : 최대 자식 수(차수)
• 모든 리프 노드는 같은 레벨에 있다.
• 루트 노드와 리프 노를 제외한 모든 노드는 M/2 이상 M 이하의 자식을 갖는다.
• 루트 노드는 적어도 2개의 자식을 갖는다.
• 각 노드의 원소수는 최소 M/2 - 1 ~ 최대 M - 1 개를 가진다.
  • 최소 개수 이하는 underflow고, 최대 개수 이상은 overflow다.
• BST와 마찬가지로 입력 자료는 중복되지 않는다.
• 각 노드의 원소는 정렬된 상태여야 한다.

😤 데이터 삽입

• 추가는 항상 리프 노드에 한다.
• 노드가 넘치면 가운데 key를 기준으로 좌우 key들을 분할하고 가운데 key는 승진한다.

[삽입 과정]

1. 트리가 비어있다면 루트 노드를 할당하고 K를 삽입한다.
2. 트리가 비어있지 않다면, 데이터를 넣을 적절한 리프 노드를 탐색한다.
3. 리프 노드에 데이터를 넣고 리프 노드가 적절한 상태에 있다면 종료한다.
4. 리프 노드가 부적절한 상태에 있다면 분리한다.

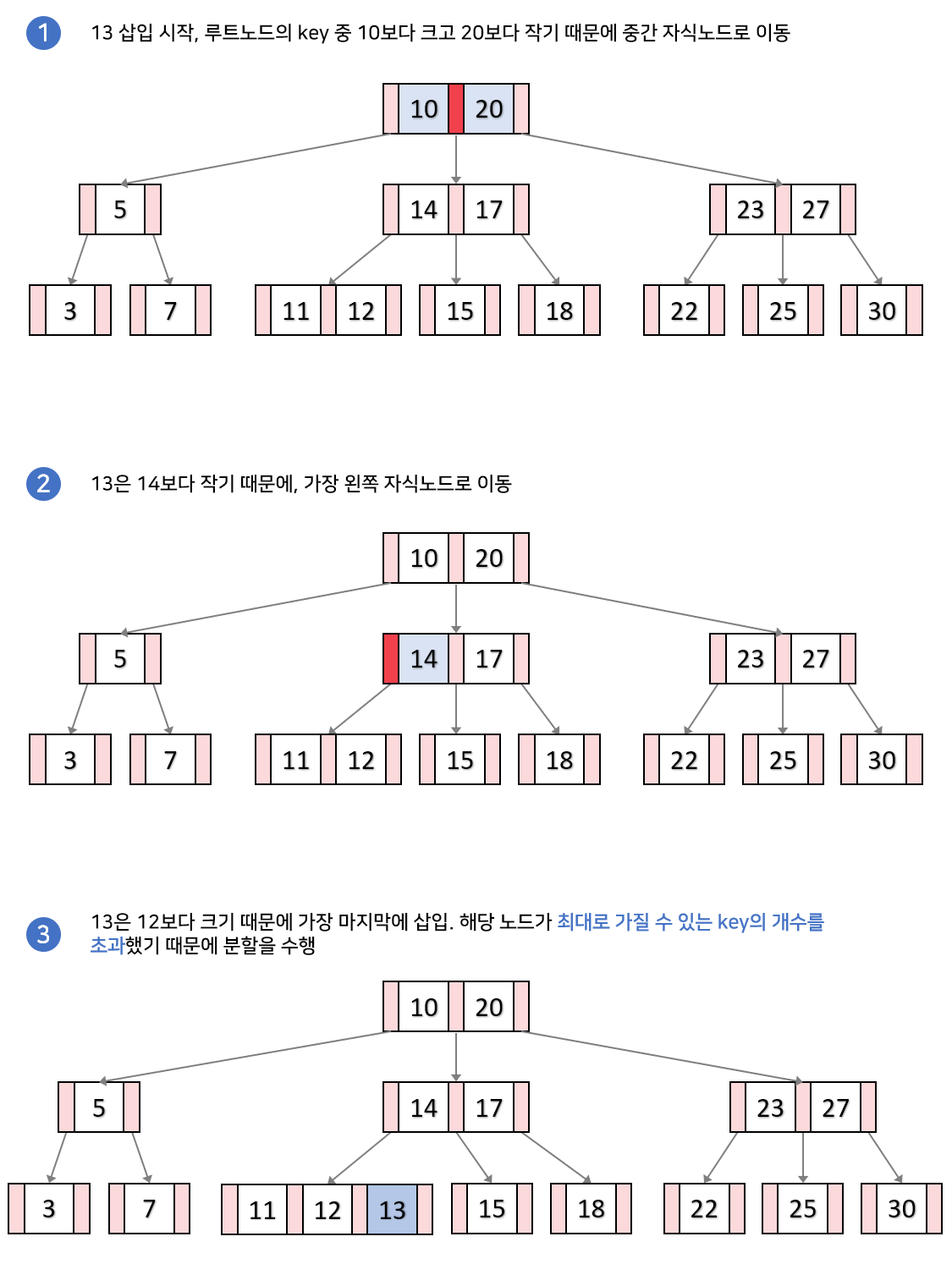
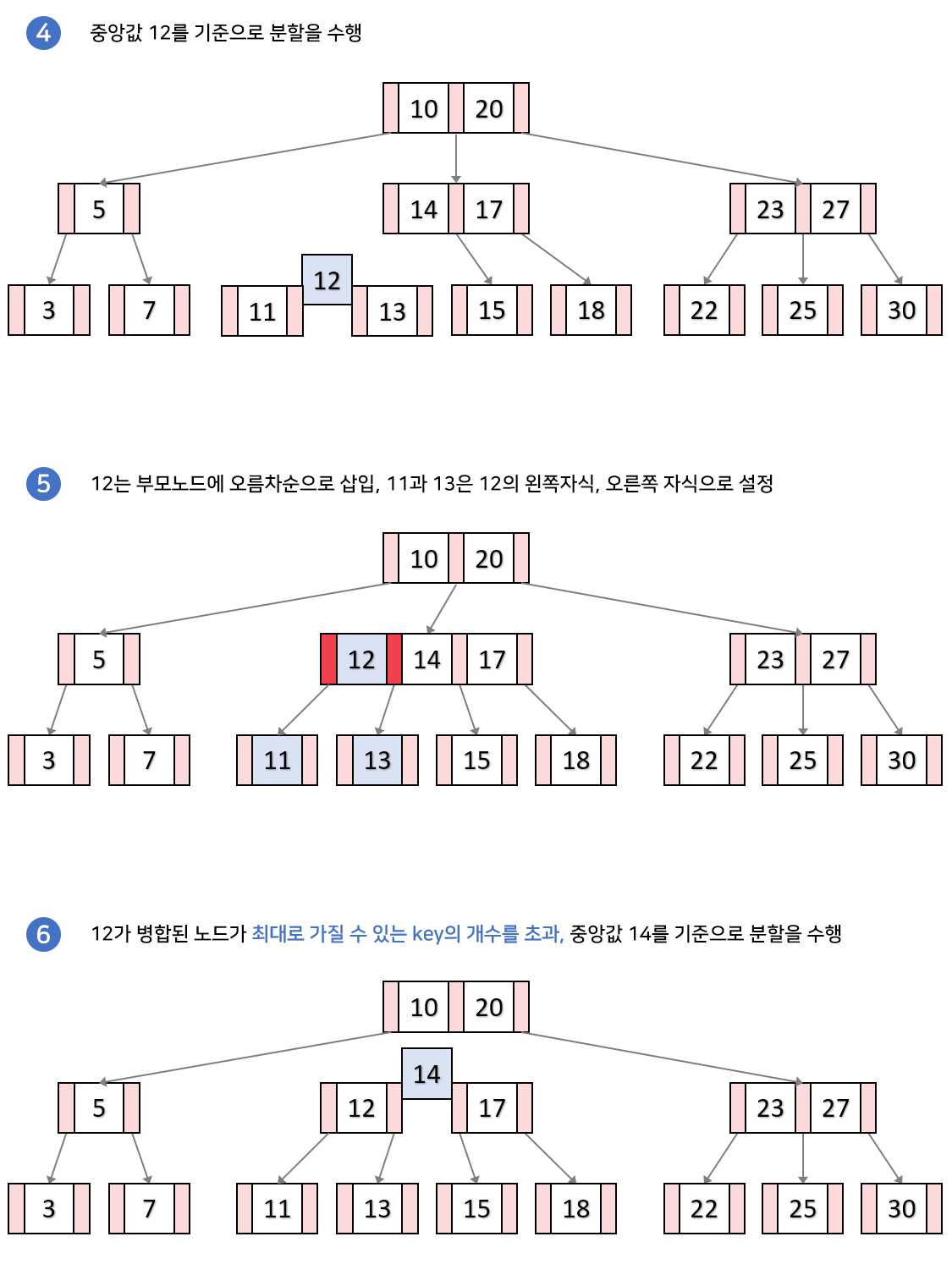
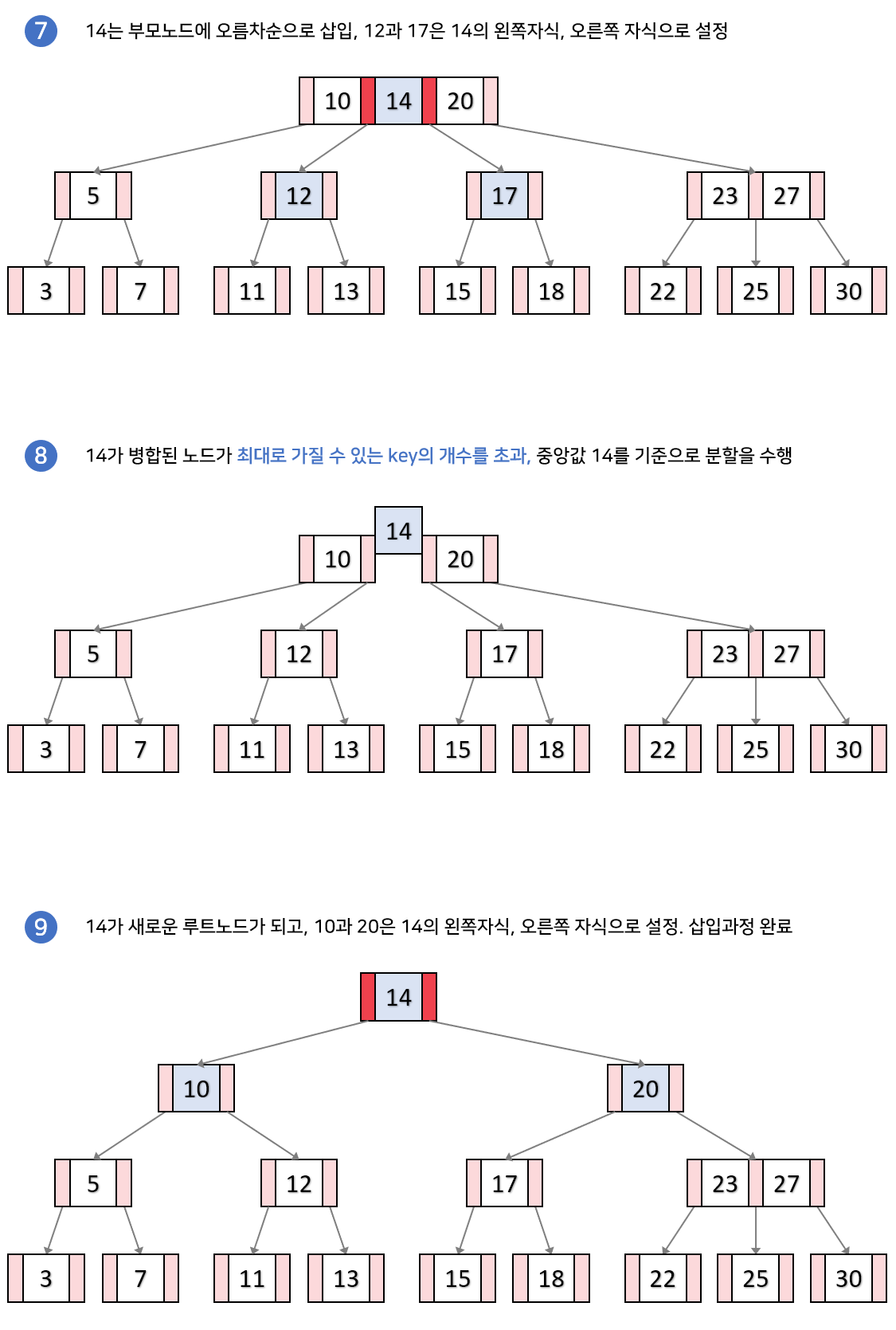
[데이터 삽입 예시]

• 차수 : 3
• 13을 삽입했을 때 연쇄적으로 분할이 일어나는 예시

😭 데이터 삭제

• 삭제도 항상 리프 노드에서 일어난다.
• 삭제 후 최소 key 수보다 적어졌다면 재조정한다.

  최소 key 수 = M/2 - 1

[재조정 과정]

1. key 수가 여유있는 형제의 지원을 받는다.
2. 1번이 불가능하면 부모의 지원을 받고 형제와 합친다.
3. 이후 부모에 문제가 있다면 부모에서 다시 재조정한다.

[데이터 삭제 예시]

• 차수 : 3

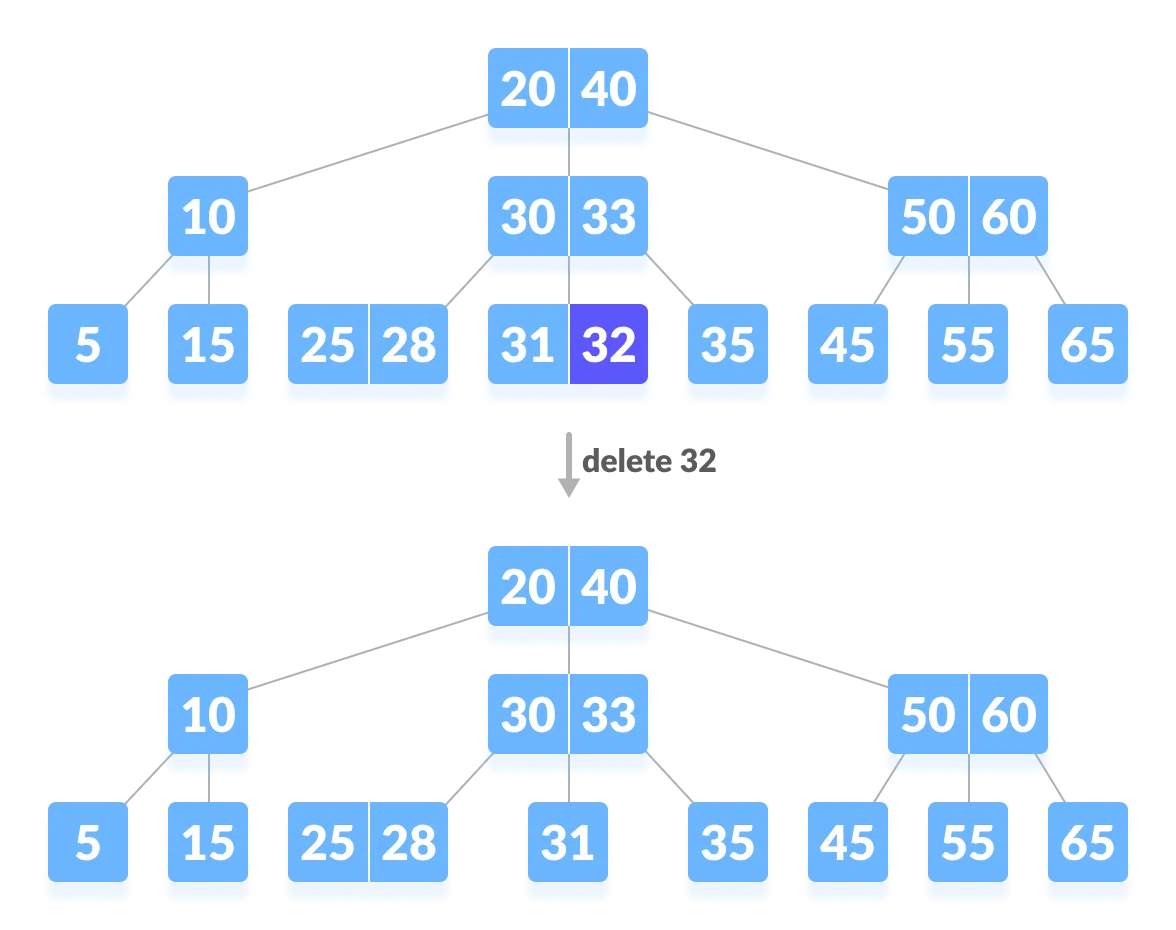
1-1. 삭제 후 재조정 필요 없는 경우

• 삭제 후에도 최소 개수 조건을 만족하므로 재조정이 일어나지 않는다.

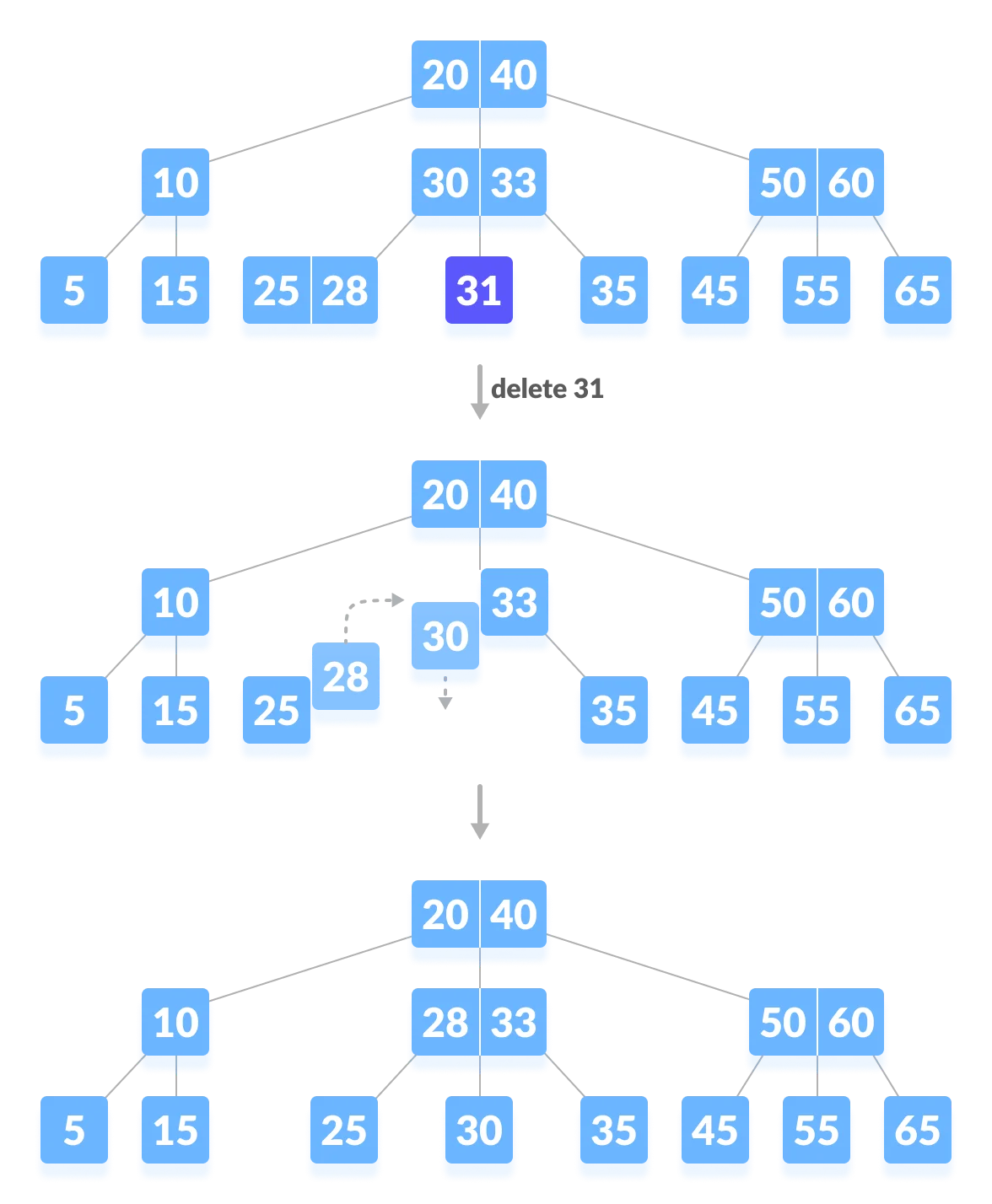
1-2. 삭제 후 재조정이 필요한 경우 - 형제의 지원 받음

• 삭제 후에 노드가 비어서 최소 조건을 만족하지 않으므로 재조정이 일어난다.
• 형제 노드에 충분한 원소 개수가 있으므로 형제 노드의 원소를 빌린다.

  형제 노드의 개수를 줄이고 자신의 노드의 개수를 늘린다.

1-3. 삭제 후 재조정이 필요한 경우 - 부모의 지원 받음

• 삭제 후에 노드가 비어서 최소 조건을 만족하지 않으므로 재조정이 일어난다.
• 형제 노드에서 원소를 빌릴 수 없으므로 부모의 지원을 받아 병합한다.

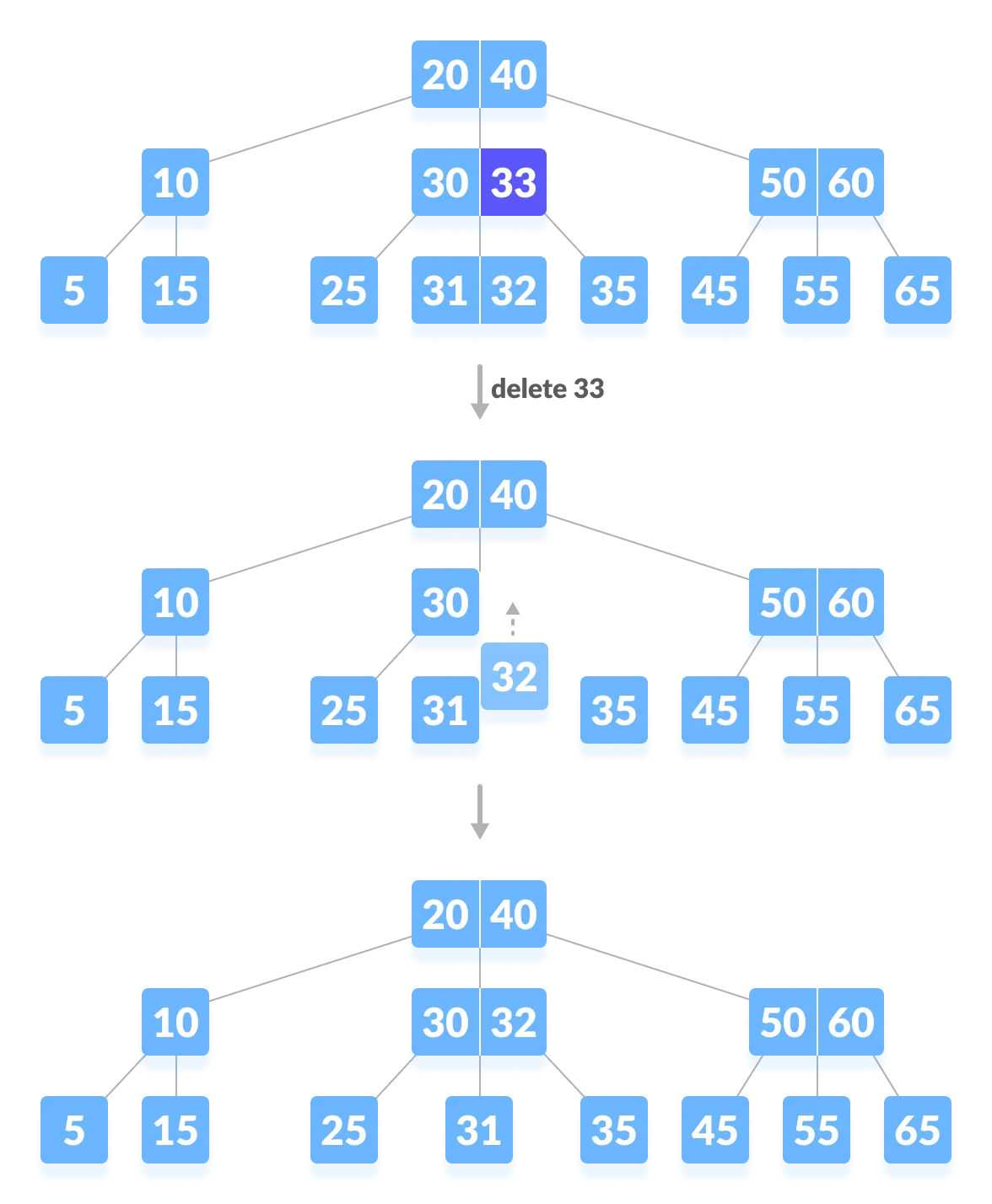
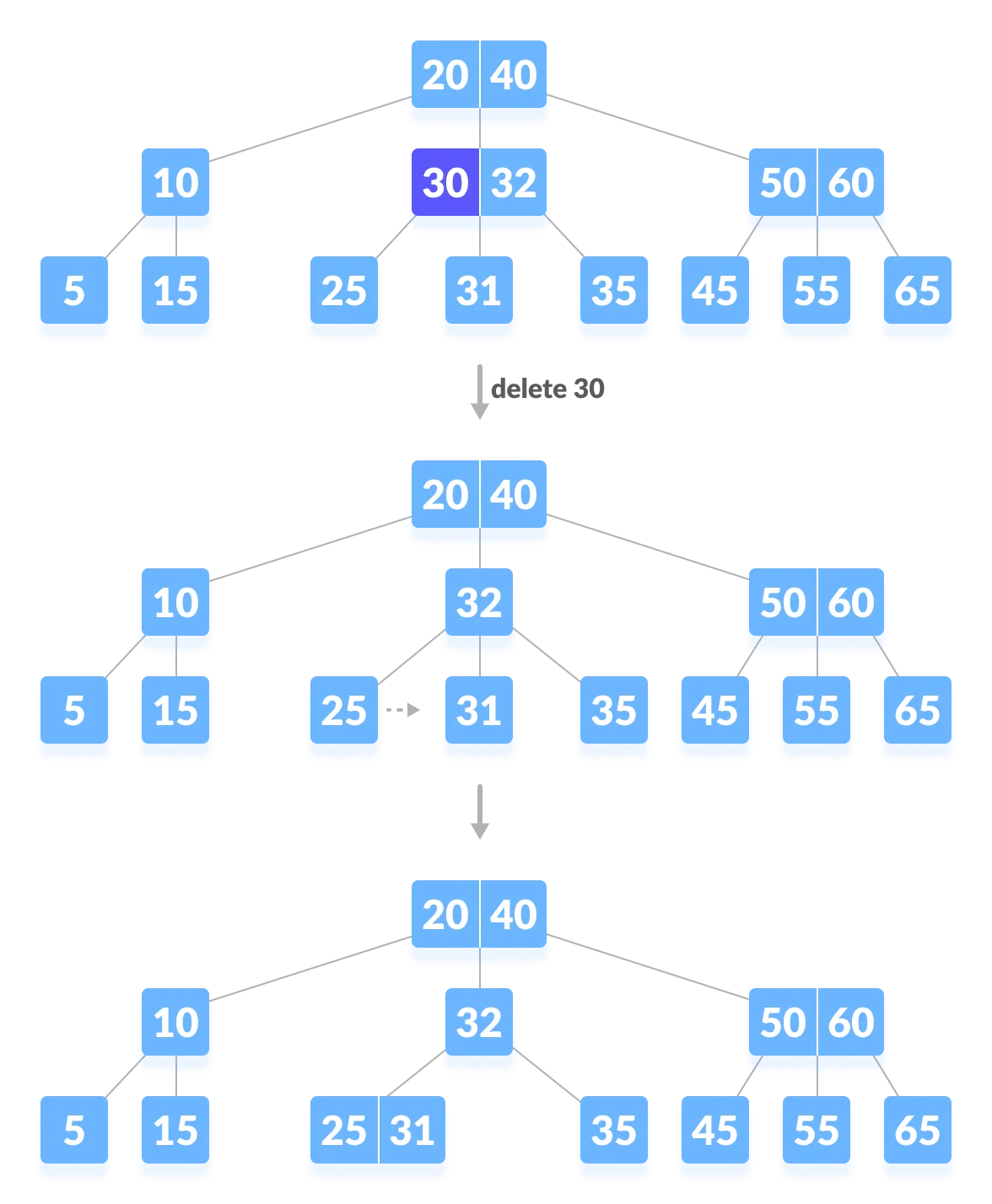
2-1. 리프 노드가 아닌 노드(internal node)의 원소를 삭제 - 자식 노드에 대체할 적합한 원소가 있는 경우

• internal node의 원소를 삭제할 때 왼쪽 자식 노드에 대체할 수 있는 원소가 있다.

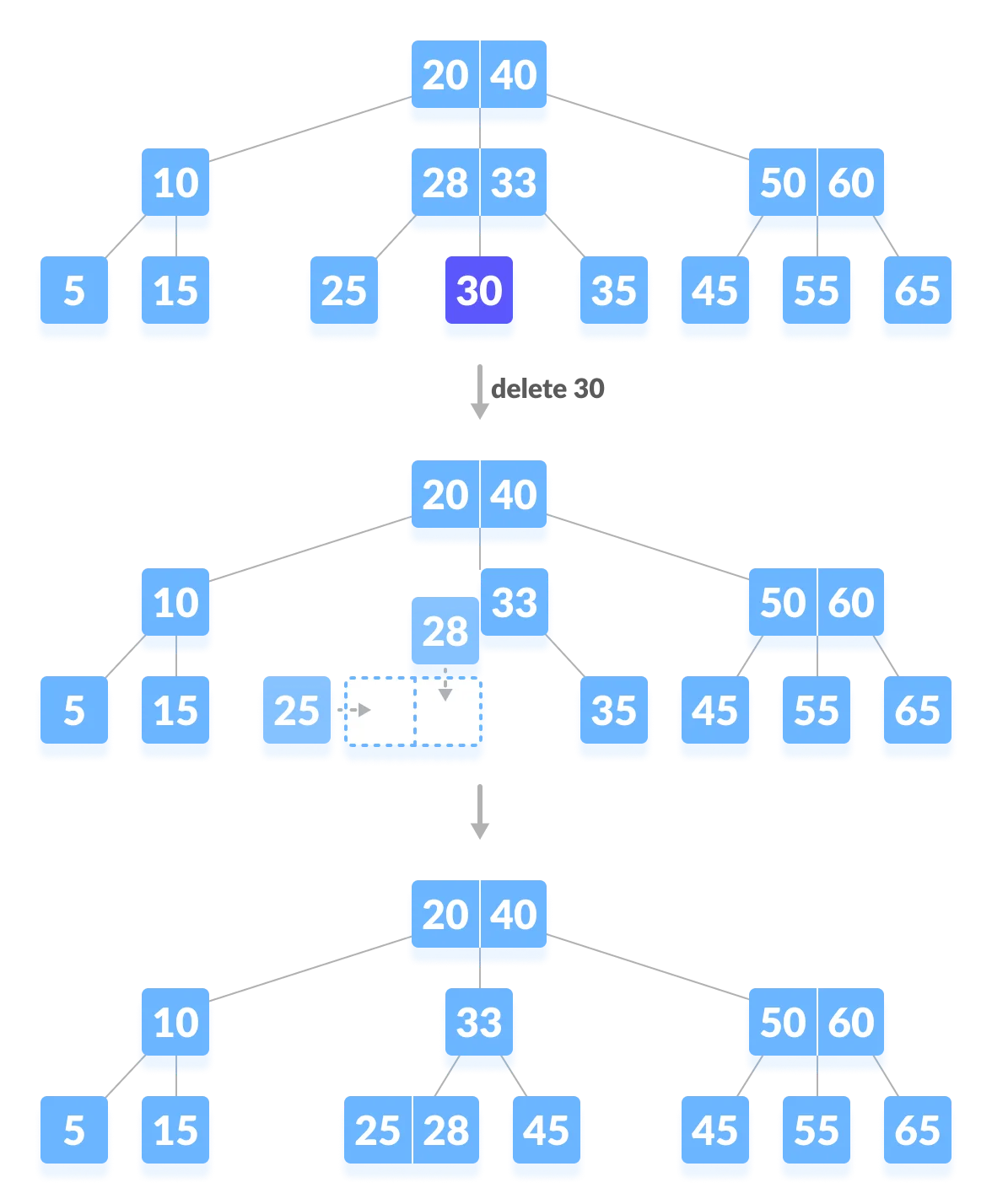
2-2. 리프 노드가 아닌 노드의 원소를 삭제 - 자식 노드에 대체할 적합한 원소가 없는 경우

• internal node의 원소를 삭제했지만 대체할 수 있는 원소가 없다.
• 왼쪽, 오른쪽 노드의 병합이 발생한다.

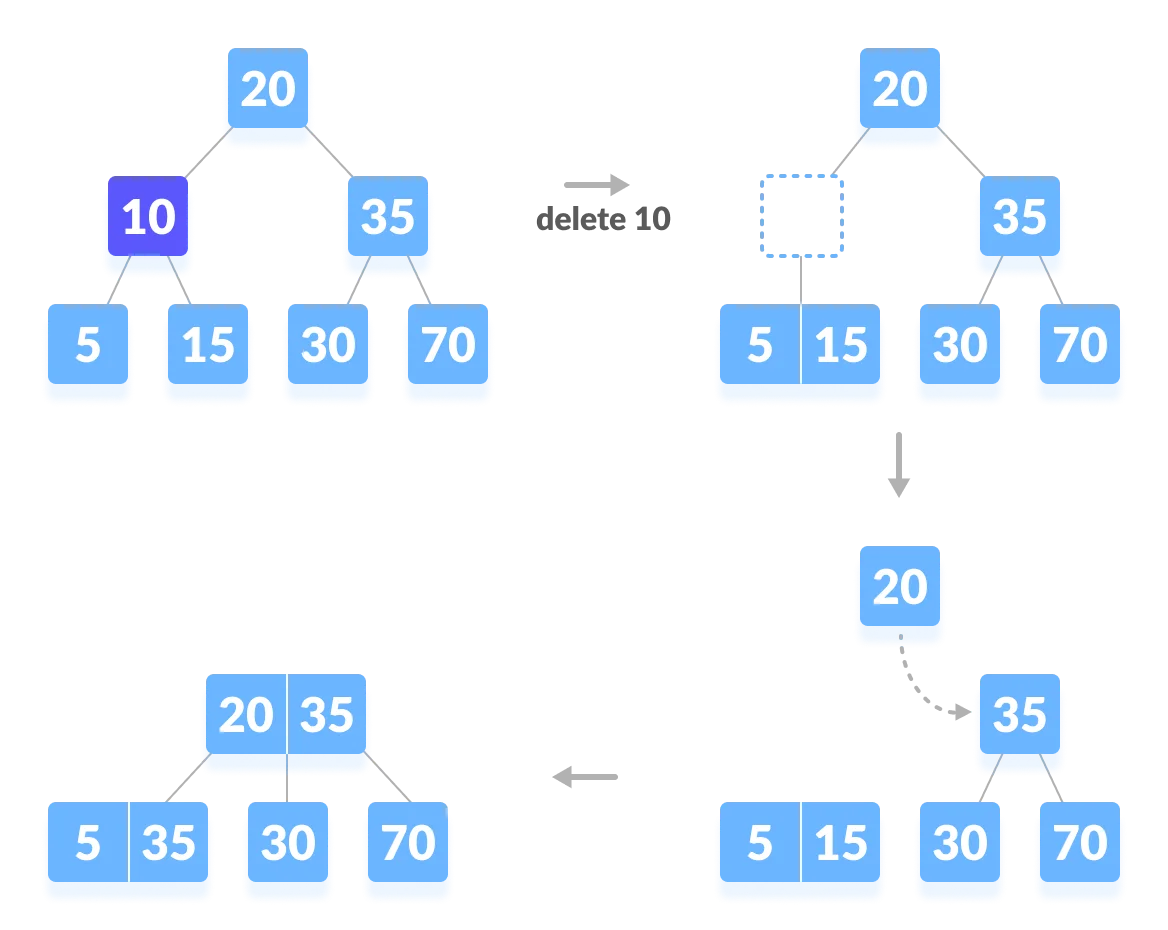
3-1. 삭제로 인해 트리의 높이가 낮아지는 경우

• 10의 삭제로 재조정이 일어나면서 트리의 높이가 낮아진다.

출처

[자료구조] 그림으로 알아보는 B-Tree

Programiz

누군가가 물어본다면

이진 탐색 트리의 높이를 낮추기 위해 여러 자식을 가질 수 있는 M원 검색 트리가 설계되었습니다.

이 M원 검색 트리에서 균형이 맞지 않아 검색 효율이 O(n) 으로 떨어진다는 문제를 해결하기 위해 B-Tree 가 설계되었습니다.

단순하고 효율적인 덕분에 현재 데이터 베이스, 파일 시스템에서 널리 사용되고 있습니다.