트리(Tree) 자료구조 알아보기

🤔 트리란?

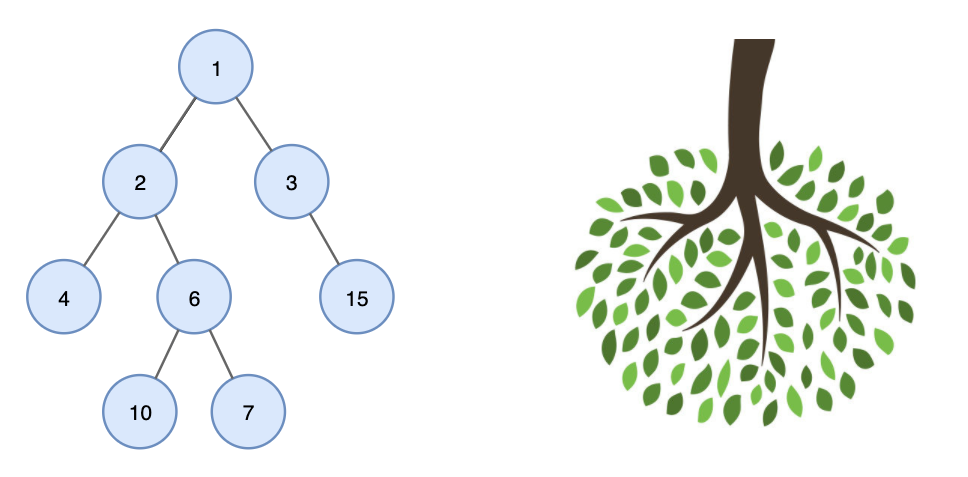
• 실제 나무를 거꾸로 세워놓은 듯한 모양이라서 트리라고 부른다.

[트리가 나온 이유]

• 일반 배열에서 삽입이나 삭제를 하는데 O(n) 의 시간이 걸린다.
• 하지만 트리는 편향된 트리가 아닌 이상 일반적인 트리에서 O(log n)으로 감소된다.

[사용사례]

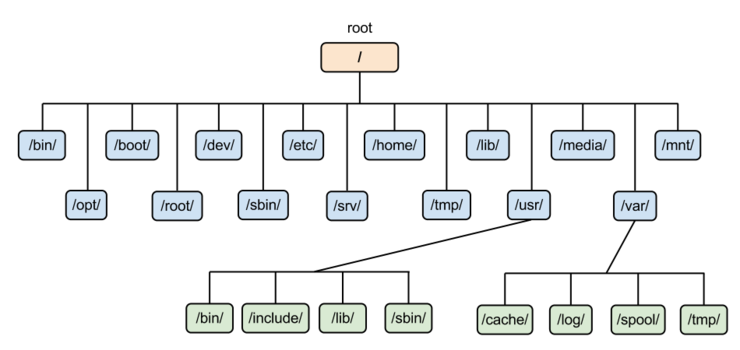
• 계층적 데이터를 저장할 때

  • 파일 및 폴더는 계층적 트리 형태로 저장된다.

    

• 효율적인 검색 속도
  • 효율적인 삽입, 삭제 및 검색을 위해 트리 구조를 사용한다.
• 힙(Heap)
  • 힙 자료구조도 트리로 구성되어 있다.
• 데이터베이스 인덱싱
  • ex. B-Tree, B+Tree, AVL-Tree 등
• Trie
  • 사전을 저장하는 데 사용되는 특별한 종류의 트리이다.

[특징]

• Tree는 Stack이나 Queue와 같은 선형 구조가 아닌 비선형 자료구조이다.
• 계층적 관계를 표현한다.
• 루트 노드를 제외한 모든 노드는 단 하나의 부모 노드만을 갖는다.
• 트리 내에 또 다른 트리가 있는 재귀적 자료구조이다.
• cycle을 갖지 않고 연결된 무방향 그래프 구조이다.
• 노드가 n개인 트리는 항상 n-1 개의 간선(edge)을 가진다.

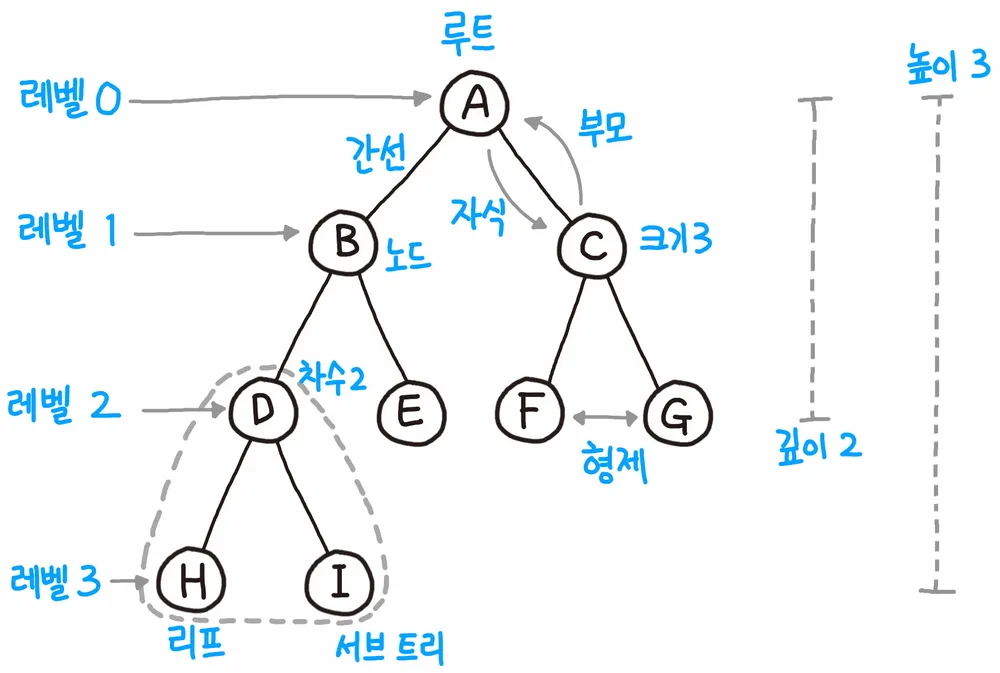
😄 트리의 구성요소

• 노드(Node) : 트리를 구성하는 각각의 요소
• 간선(Edge) : 트리를 구성하기 위해 노드와 노드를 연결하는 선
• 루트 노드(Root Node) : 트리 구조에서 최상위에 있는 노드

  A

• 부모 노드(Parent Node) : 자식 노드를 가진 노드

  H, I의 부모 노드는 D

• 자식 노드(Child Node) : 부모 노드의 하위 노드

  D의 자식 노드는 H, I

• 형제 노드(Sibling Node) : 같은 부모를 가지는 노드

  F와 G

• 외부 노드(External Node), 단말 노드(Terminal Node), 리프 노드(Leaf Node) : 자식 노드가 없는 노드

  H, I, E, F, G

• 내부 노드(Internal Node), 비단말 노드(Non-Terminal Node), 가지 노드(Branch Node) : 자식 노드를 하나 이상 가진 노드

  A, B, C, D

• 깊이(Depth) : 루트에서 어떤 노드까지의 간선(Edge) 수

  루트 노드 : 0, D : 2

• 높이(Height) : 어떤 노드에서 리프 노드까지 가장 긴 경로의 간선(Edge) 수

  3

• 레벨(Level) : 루트에서 어떤 노드까지의 간선(Edge) 수

🌲 트리의 종류

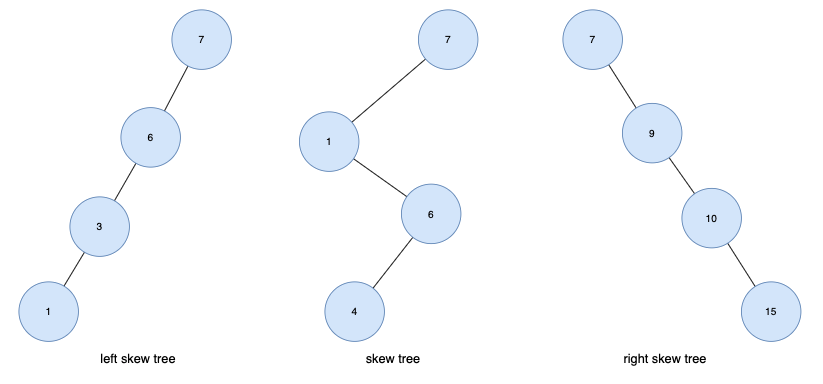
[편향 트리(Skew Tree)]

• 모든 노드들이 자식을 하나만 가지는 트리
• 왼쪽 방향으로만 가지면 left skew tree, 오른쪽 방향으로만 가지면 right skew tree 라고 한다.

[이진 트리(Binary Tree)]

• 각 노드의 차수(자식 노드)가 2 이하인 트리

• 루트 노드를 중심으로 두 개의 서브 트리로 나뉘어지고 이 서브 트리들 또한 모두 이진 트리여야 한다.

• 포화 이진 트리(Full Binary Tree) : 모든 레벨이 꽉 찬 이진 트리
• 완전 이진 트리(Complete Binary Tree) : 왼쪽에서 오른쪽으로 순서대로 차곡차곡 채워진 이진 트리

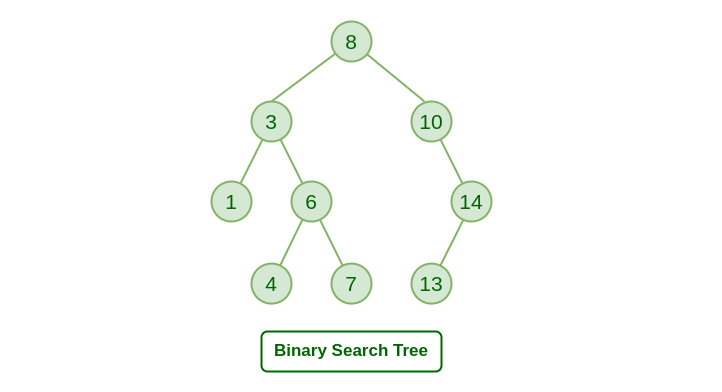
[이진 탐색 트리(Binary Search Tree, BST)]

• 순서화된 이진 트리
• 노드의 왼쪽 자식은 부모의 값보다 작은 값을 가져야 하며 노드의 오른쪽 자식은 부모의 값보다 큰 값을 가져야 한다.

누군가가 물어본다면

트리는 삽입/삭제 에서 O(log n)이 소요되는 자료구조이고 디렉토리 구조와 같은 계층적 구조에서 주로 사용됩니다.

각 노드의 자식 노드가 2개 이하이면 이진 트리, 왼쪽 자식이 부모값보다 작고 오른쪽 자식이 부모값보다 큰 이진 트리는 이진 탐색 트리, 즉 BST 라고 부릅니다.