힙(heap) 자료구조 알아보기

🤔 힙(Heap) 이란?

• 완전 이진 트리 의 일종으로 우선순위 큐를 위해 만들어진 자료구조이다.
• 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다.
• 이진 탐색 트리는 중복 값을 허용하지 않지만 힙은 중복 값을 허용한다.

메모리의 힙(heap) 영역과는 다른 개념이다!

[우선순위 큐]

• 데이터들 중 우선순위가 가장 높은 데이터가 먼저 나간다.

  자료 구조	먼저 나가는 요소
  스택(Stack)	가장 최근에 들어온 데이터(LIFO)
  큐(Queue)	가장 먼저 들어온 데이터(FIFO)
  우선순위 큐(Priority Queue)	가장 우선순위 가 높은 데이터

• 시뮬레이션 시스템, 작업 스케쥴링, 수치해석 계산 등에 사용된다.
• 우선 순위 큐는 배열, 연결 리스트, 힙으로 구현된다.

• 이 중 힙으로 구현하는 것이 가장 효율적이다.

  우선순위 큐 구현방법	삽입	삭제
  순서 없는 배열	O(1)	O(n)
  순서 없는 연결 리스트	O(1)	O(n)
  정렬된 배열	O(n)	O(1)
  정렬된 연결 리스트	O(n)	O(1)
  힙(heap)	O(log n)	O(log n)

🤗 힙(heap)의 종류

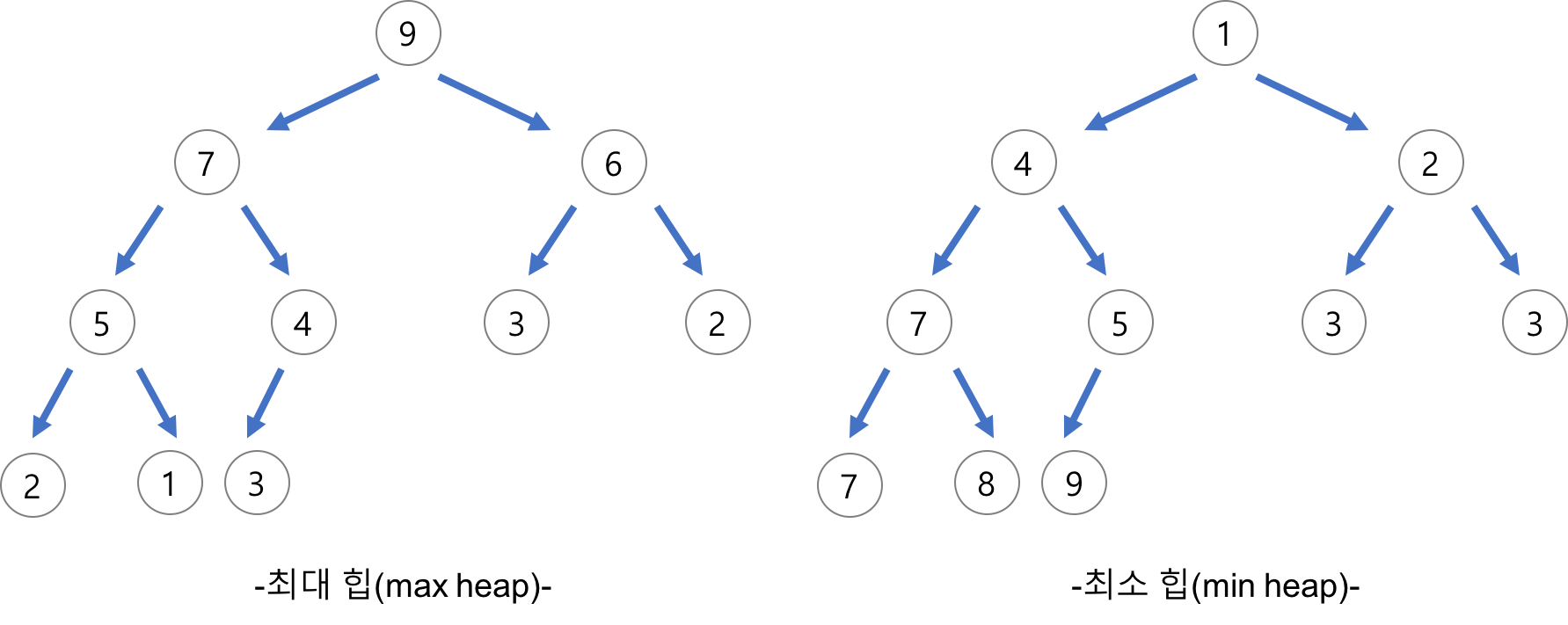
[최대 힙(max heap)]

• 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
• key(부모) >= key(자식)

[최소 힙(min heap)]

• 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
• key(부모) <= key(자식)

😎 힙(heap)의 구현

• 힙을 저장하는 표준적인 자료구조는 배열이다.
• 쉬운 구현을 위해 배열의 첫 번째 인덱스인 0은 사용되지 않는다.
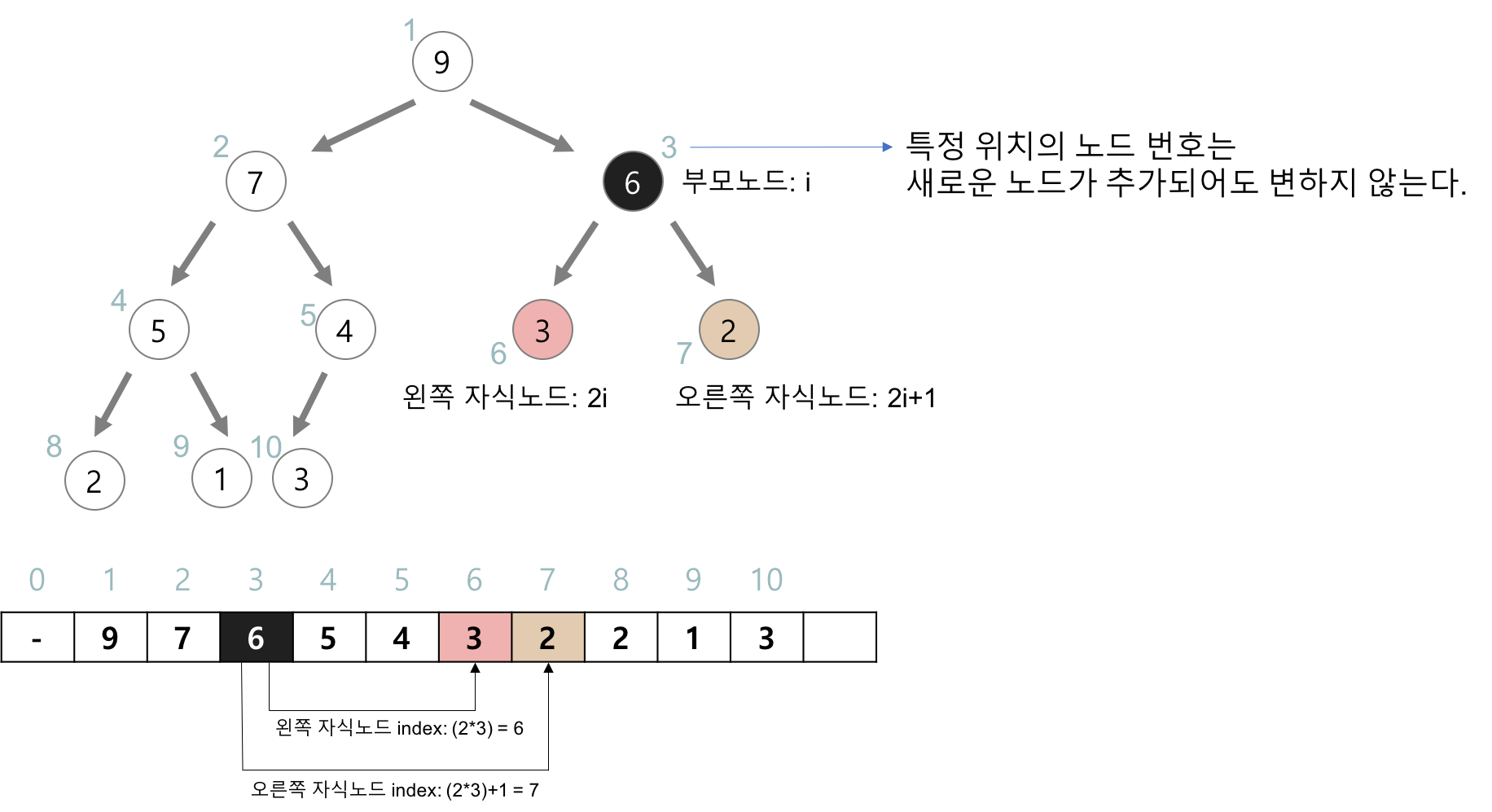
• 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다.

[부모 노드와 자식 노드의 관계]

• 왼쪽 자식의 인덱스 = (부모 인덱스) * 2
• 오른쪽 자식의 인덱스 = (부모 인덱스) * 2 + 1
• 부모 인덱스 = (자식 인덱스) / 2

[자바에서의 힙 구현]

• 위에서 말했듯이 힙은 우선순위 큐 구현을 위한 자료구조로, 우선순위를 사용하면 최소힙 자료구조를 기본으로 사용한다.
• 만약 최대힙을 사용하고 싶다면 정렬기준을 반대로 주면 된다.

PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());

삽입, 삭제에서는 우선순위 큐가 아닌 순수 힙 배열을 통해 알아보겠다.

[삽입]

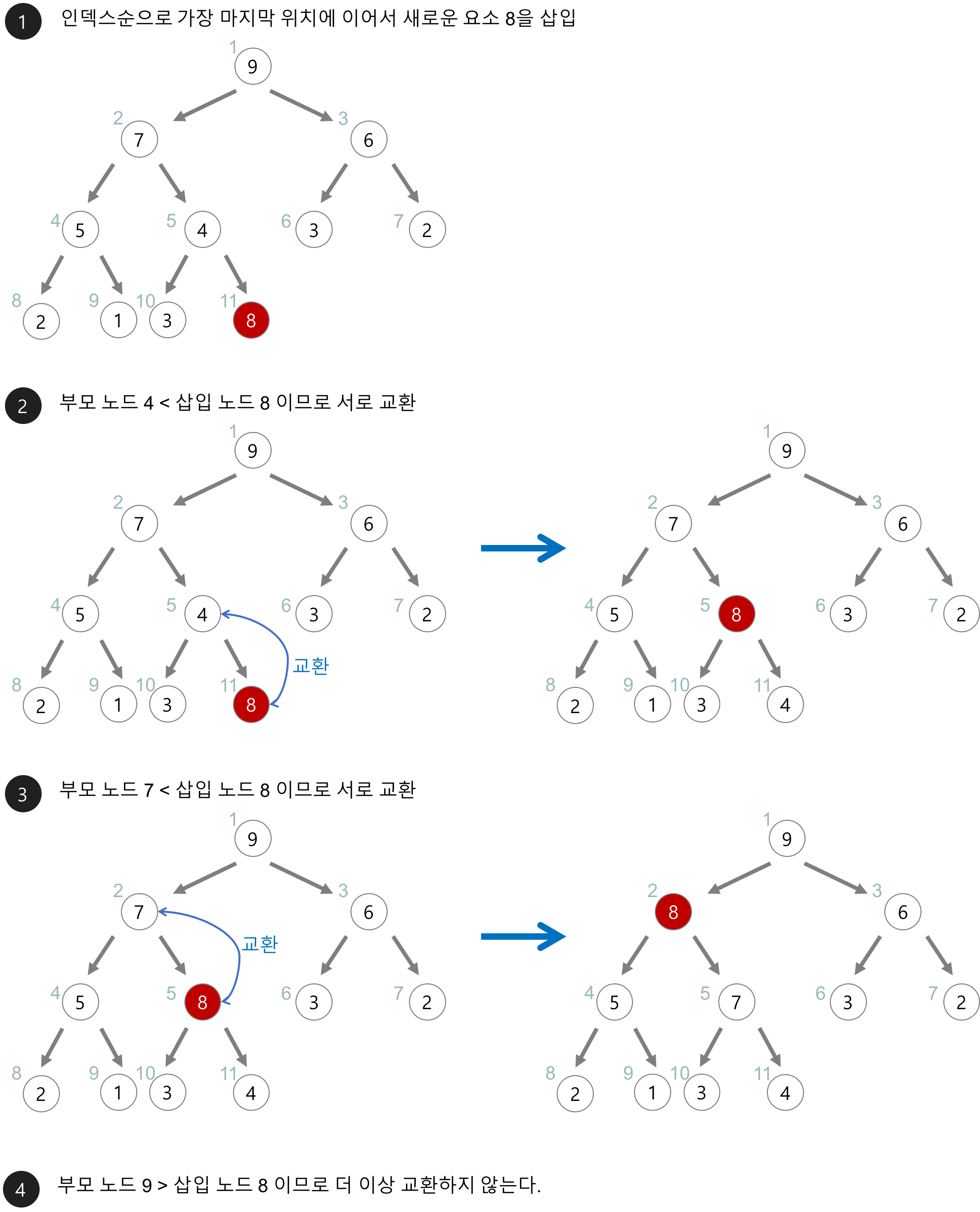
• 힙에 새로운 요소가 들어오면 일단 새로운 노드를 힙의 마지막 노드에 삽입한다.
• 새로운 노드와 부모 노드의 크기 비교를 한 후 부모 노드와 교환한다.

int[] maxHeap = new int[12];
int nowHeapSize = 0;

void insertMaxHeap(int x){
    maxHeap[++nowHeapSize] = x;
    // 힙 크기를 하나 증가시키고, 마지막 노드에 x를 삽입

    for(int i=nowHeapSize; i>1 ; i--){
        // 마지막 노드가 자신의 부모 노드보다 크면 swap 한다.
        if(maxHeap[i/2] < maxHeap[i]){  // 자식 인덱스 / 2 = 부모 인덱스
            swap(i/2, i);
        }else{
            break;
        }
    }
}

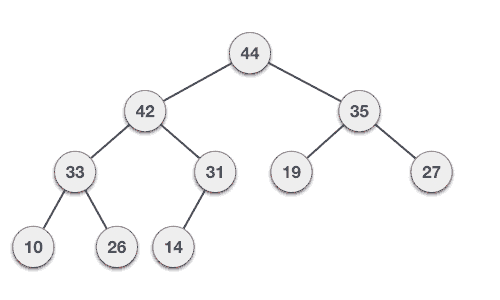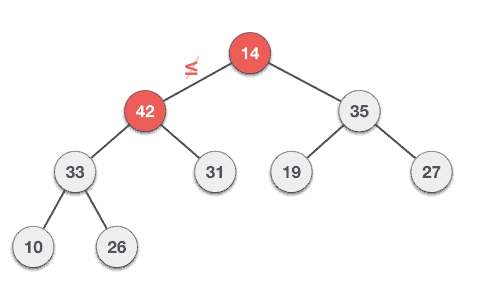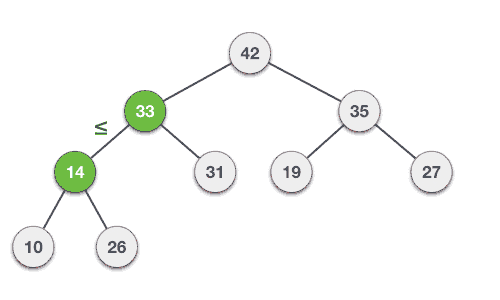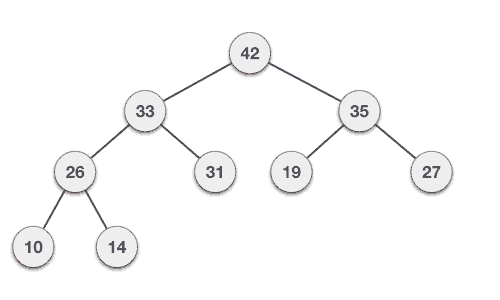
[삭제]

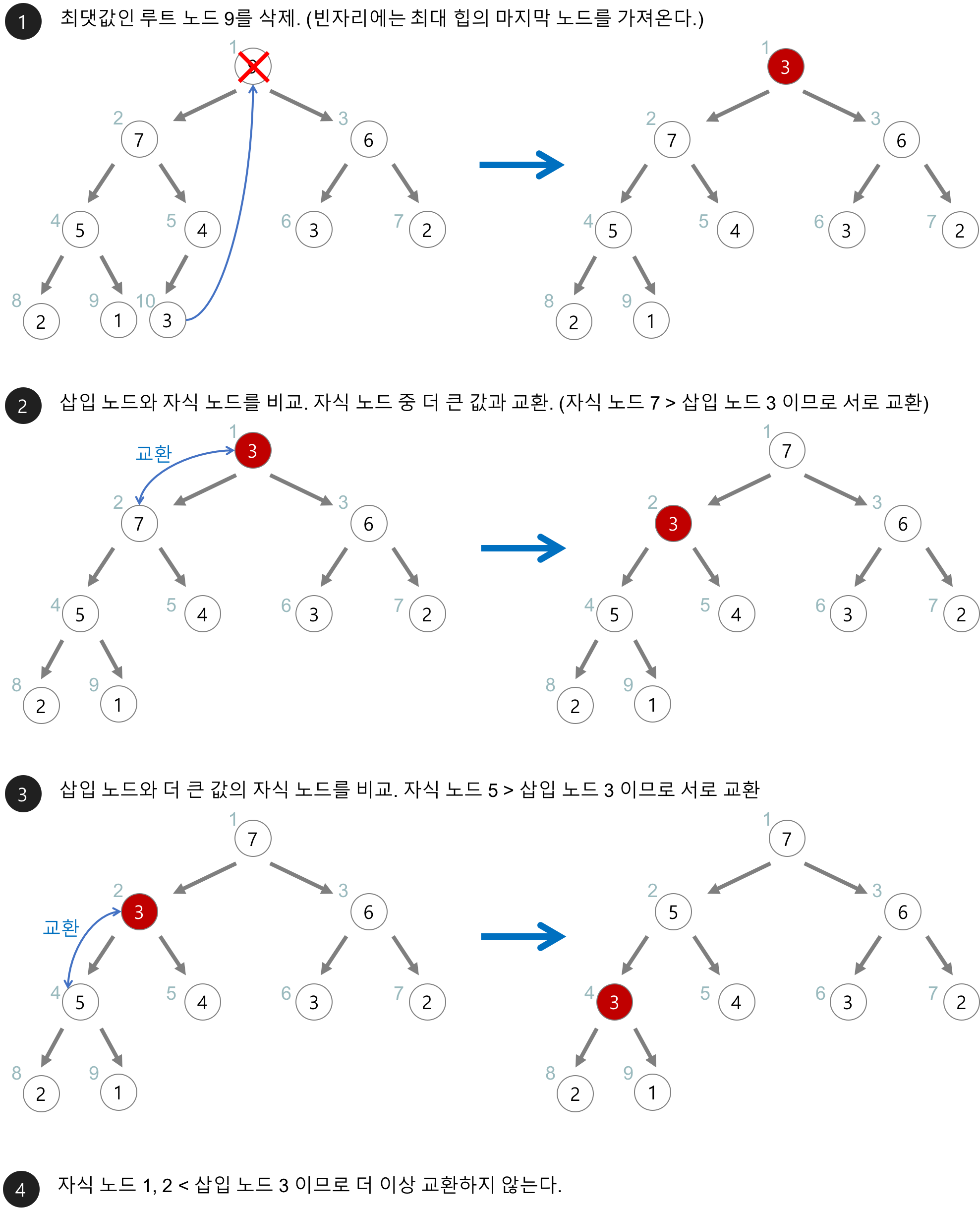
• 최대힙에서 최댓값은 루트 노드(인덱스 1) 이므로 루트 노드가 삭제된다.
• 삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
• 힙을 재구성한다.

int deleteMaxHeap(){
    if(nowHeapSize == 0)    // 비어있는 경우
        return 0;

    int root = maxHeap[1];  // 루트 노드 값 저장
    maxHeap[1] = maxHeap[nowHeapSize];  // 마지막 노드를 루트 노드로 이동
    maxHeap[nowHeapSize--] = 0; // 힙 크기를 하나 줄이고 마지막 노드를 0으로 초기화

    // 힙을 재구성하는 로직
    for(int i=1; i*2 <= nowHeapSize;){
        // 마지막 부모 노드가 왼쪽, 오른쪽 자식 노드들보다 크면 끝
        if(maxHeap[i] > maxHeap[i*2] && maxHeap[i] > maxHeap[i*2+1]){
            break;
        }else if(maxHeap[i] < maxHeap[i*2]){    // 왼쪽 자식 노드가 부모보다 더 큰 경우
            swap(i, i*2);
            i = i*2;
        }else{  // 오른쪽 자식 노드가 부모보다 더 큰 경우
            swap(i, i*2+1);
            i = i*2+1;
        }
    }

    return root;
}

[Heapify]

• 두 개의 서브 트리가 최대힙/최소힙 일 때, root를 포함하는 전체가 heap이 되도록 위치를 조정하는 과정을 말한다.
• 루트에서 작은 값이 흘러 내려가면서 처리되는 방식으로 진행된다.
• 최대힙의 경우 root가 child보다 작으면 두 개의 child node 중 값이 큰 노드를 root와 교체하고 교체할 노드가 없을 때까지 반복한다.

누군가가 물어본다면

힙 자료구조는 완전 이진 트리의 일종으로 우선순위 큐를 위해 만들어졌습니다.

여러 개의 값들 중에서 최댓값 또는 최솟값을 빠르게 찾아낼 수 있습니다.