DP - Dynamic Programming

🤔 DP 란?

• Dynamic Programming(동적 계획법)

  사실 이름은 멋있어 보여서 지은 것이라고 한다.

• 복잡한 문제를 재귀적으로 나누어 해결하는 방식
• 각 하위 문제의 해결 결과를 저장해두고 필요할 때 다시 사용(메모제이션)하여 효율적으로 문제를 해결할 수 있다.
• 재사용하기 때문에 계산의 중복을 피하여 좋은 성능을 보인다.
• 핵심은 큰 문제를 작은 문제로 쪼개서 그 답들을 저장해두고 재활용하는 것이다.

🤨 재귀와의 차이

• 재귀 또한 마찬가지로 작은 문제로 쪼개서 풀어나가지만 기존 답을 재활용 하지 않는다는 차이가 있다.
• 피보나치 수열을 예로 재귀로 함수를 구성하면 f(n) = f(n-1) + f(n-2) 이다.
• 만약 100번째 피보나치 수를 구하려면 f(1)의 호출 횟수는 세기 힘들 정도로 굉장히 많다.
• 반면에 DP로 구하면 f(1)의 호출 횟수는 단 한번이다.

🤗 DP의 사용 조건

• DP를 적용하려면 다음 2가지 조건을 만족해야 한다.

1. Overlapping Subproblems(겹치는 부분 문제)
2. Optimal Substructure(최적 부분 구조)

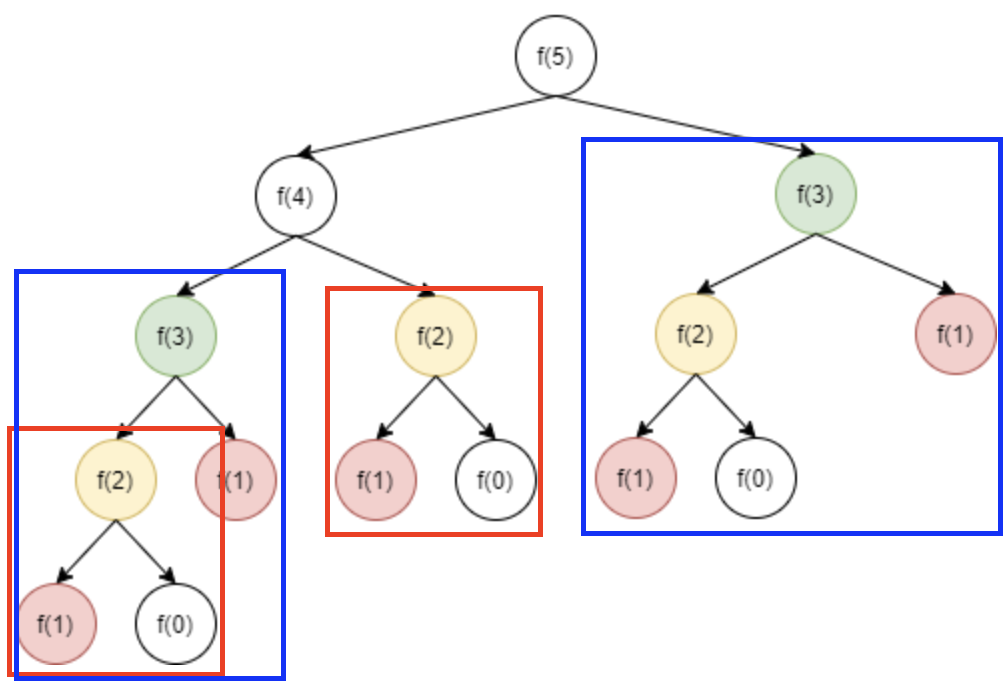
[Overlapping Subproblems(겹치는 부분 문제)]

• DP는 문제를 나누고 그 문제의 결과 값을 재활용해서 전체 답을 구한다. 따라서 재활용하기 위해선 동일한 작은 문제들이 반복하여 나타나야 한다.

• 위 그림과 같이 동일한 부분 문제가 중복되어서 나타나야 한다. 이러한 경우에 저장된 값을 재활용 할 수 있고 DP를 사용할 수 있다.

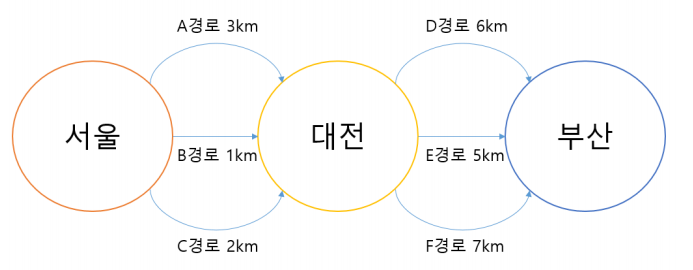
[Optimal Substructure(최적 부분 구조)]

• 위 그림에서 서울에서 부산까지 제일 짧은 거리를 구하기 위해서는 서울-대전 거리의 최솟값, 대전-부산 거리의 최솟값을 각각 구하여 합치면 된다.
• 이렇게 부분 문제의 최적 결과 값이 전체 문제의 최적 결과를 낼 수 있는 경우를 최적 부분 구조 라고 한다.

😤 DP는 어떻게 풀어야하는가

• 코딩테스트에서 DP는 어떻게 풀어야 할까?

  DP 문제임을 알아차리기, 구현 방식 등은 넘어가겠다.

• 신입 공채 코딩테스트의 경우 문제들의 난이도는 아무리 높아도 골드 1이고, DP 문제들의 경우 골드3 정도가 최대인 것 같다.
• DP 문제들의 핵심은 점화식을 찾을 수 있는지 여부이다.
• 코딩테스트 환경에서 노트로 필기하는 것은 허용되므로 DP 문제임을 안 순간부터 노트를 사용하여 직접 경우를 따져보는게 가장 빠른 해결법이라고 본다.
• 가장 간단한 경우부터 4~5개 정도의 경우를 차례대로 따져보고 점화식을 구한다음 코드에 녹여내는 연습을 한다면 실전에서 큰 문제 없이 해결할 수 있다고 생각한다.

BOJ 2133 - 타일 채우기 (골드 4)

2133-타일 채우기

• 3xN 크기의 벽을 2x1, 1x2 두 종류의 타일로 채울 수 있는 경우의 수를 구하는 문제이다.
• n이 홀수인 경우 벽의 크기 3xn 도 홀수이므로 크기가 2인 타일들로는 채울 수 없으므로 경우의 수는 0이다.
• n = 2, 4, 6, 8 일 때의 경우의 수를 직접 따져본다.

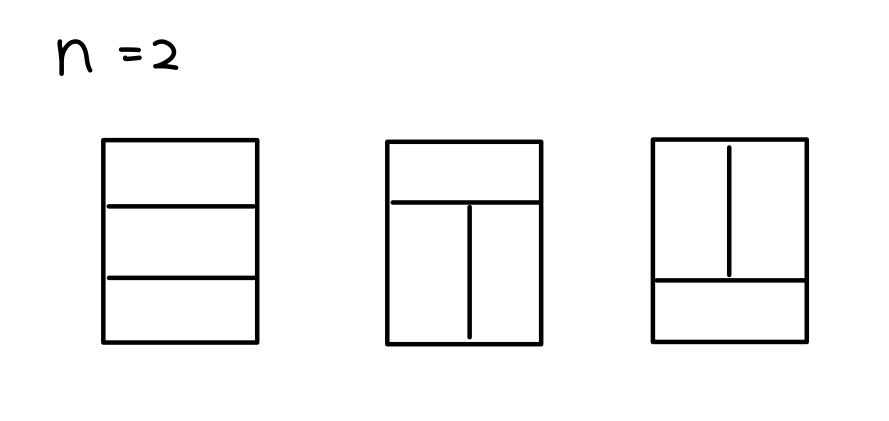
[n=2]

• n=2 인 경우 위 그림처럼 3가지 경우밖에 없다.

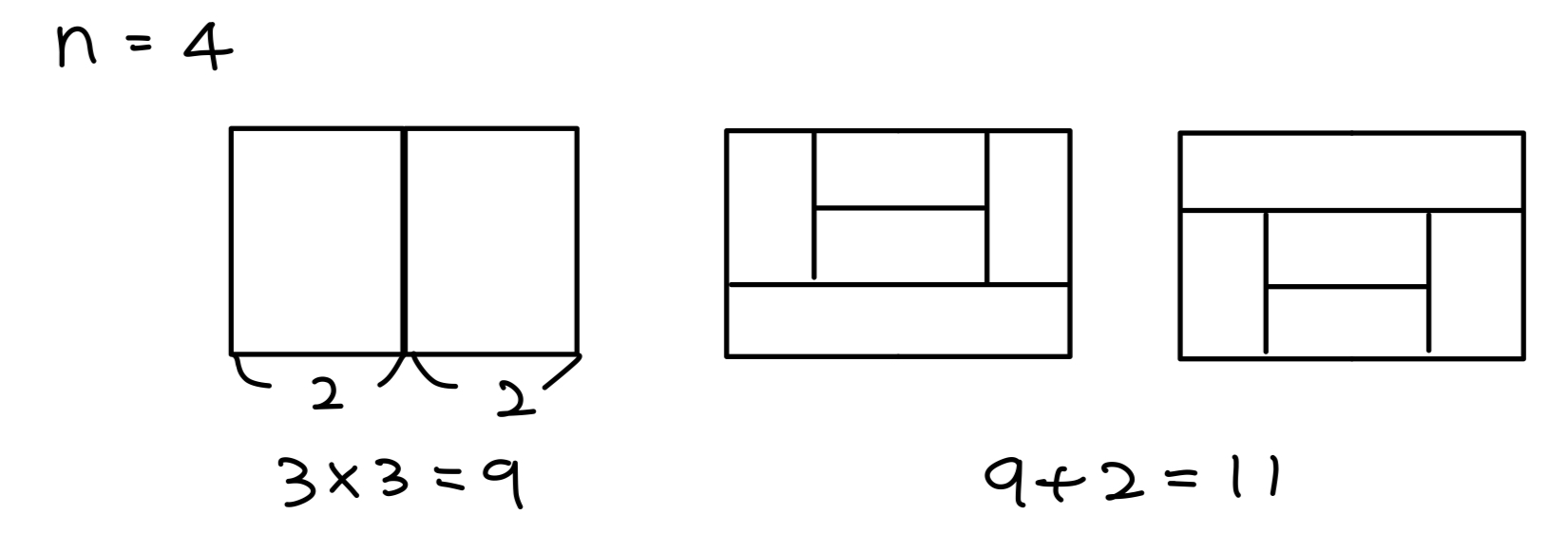
[n=4]

• n=2인 경우를 이어붙인 경우 9가지
• 이에 해당되지 않는 예외 경우 2가지
• 총 11가지가 나온다.

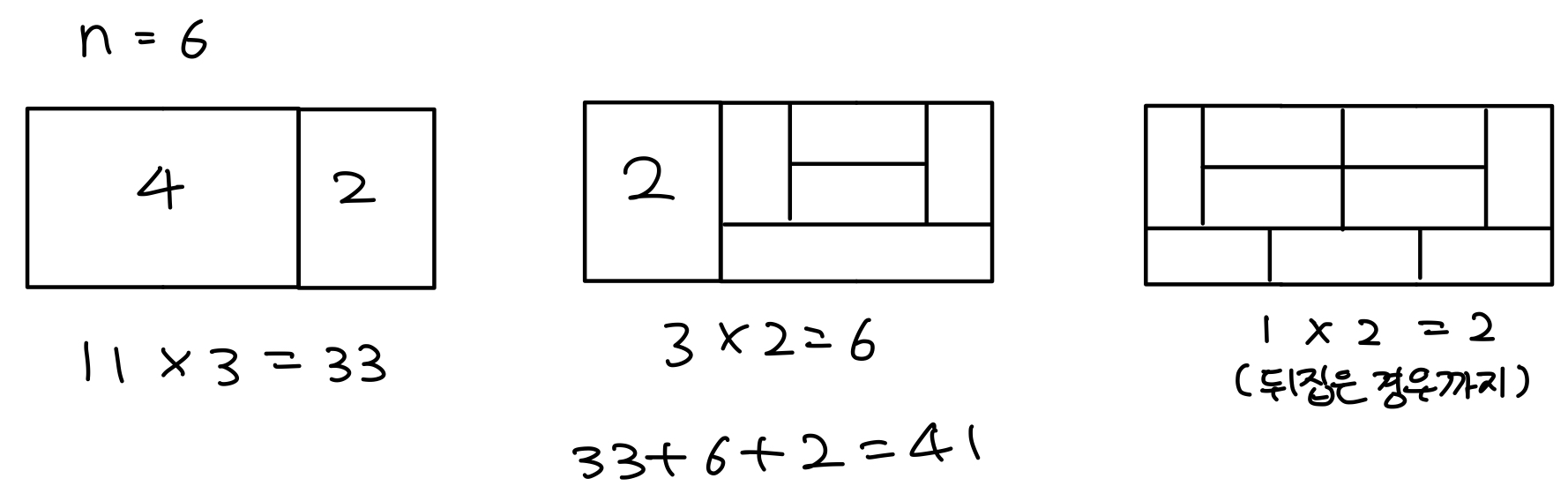
[n=6]

• n=4인 경우에서 n=2인 경우를 곱한 33가지
• n=4의 예외 경우와 n=2 경우를 곱한 6가지
• n=6의 새로운 예외 2가지
• 총 41가지가 나온다.
• 점점 규칙이 보이는 것 같다.

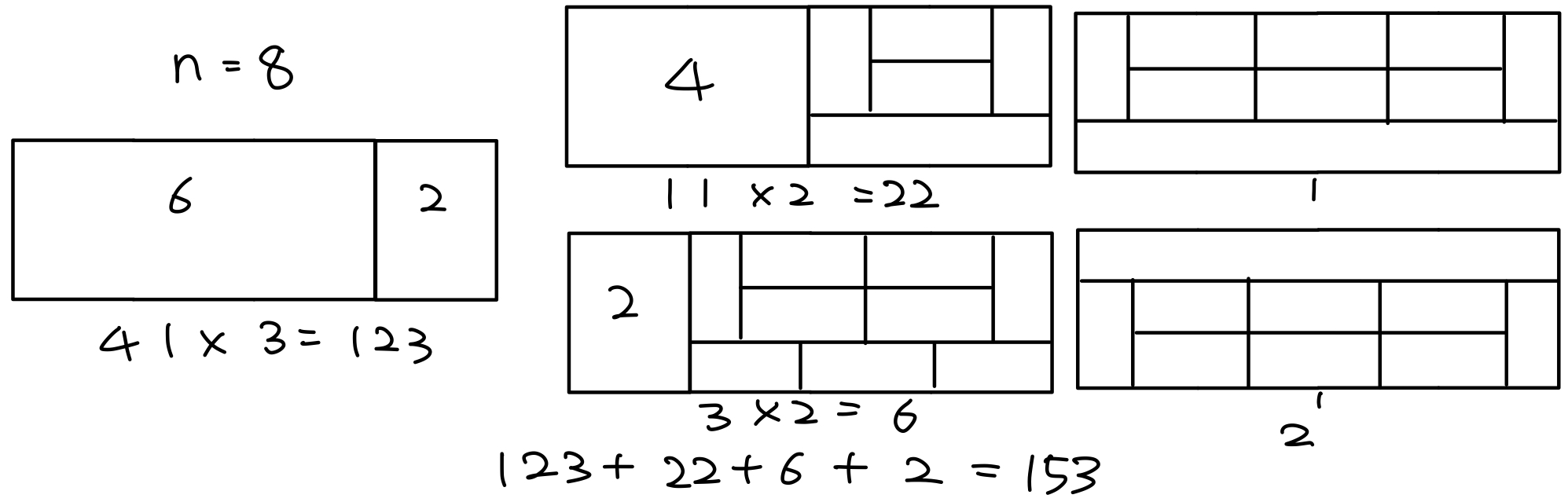
[n=8]

• n=6인 경우에서 n=2인 경우를 곱한 123가지
• n=4의 예외 경우와 n=4 경우를 곱한 22가지
• n=6의 예외 경우와 n=2 경우를 곱한 6가지
• n=8의 새로운 예외 2가지
• 총 153가지가 나온다.

규칙 정리

1. n-2 경우의 수에 n=2인 경우의 수(3)을 곱한 경우의 수가 나온다.
2. 이전 경우들에서 발생한 예외 경우들에 빈 공간을 곱한 경우의 수가 나온다.
3. n >= 4 에서 매번 새로운 예외 2가지가 나온다.
   • 이를 식으로 정리하면 다음과 같다.

1. f(n-2) * 3
2. f(n-4) * 2 + f(n-6) * 2 + ... + f(2) * 2
3. 2

=> f(n) = 3f(n-2) + 2(f(n-4)+...+f(2)) + 2 (n>=4)

import java.io.*;
import java.util.*;

public class Main {
    static FastReader scan = new FastReader();
    static StringBuilder sb = new StringBuilder();

    static int n;
    static int[] dp;

    public static void main(String[] args) {
        input();
        solve();
    }

    static void input() {
        n = scan.nextInt();
    }

    static void solve() {

        if (n == 1) {
            System.out.println(0);
            return;
        }

        dp = new int[n+1];

        dp[0] = 0;
        dp[1] = 0;
        dp[2] = 3;

        for (int i = 3; i <= n; i++) {
            if (i % 2 == 1) {
                dp[i] = 0;
            }else{
                dp[i] += 2 + dp[i - 2] * 3;
                for (int j = i-4; j >= 2; j -= 2) {
                    dp[i] += dp[j]*2;
                }
            }
        }

        System.out.println(dp[n]);
    }

    static class FastReader {
        .
        .
        .
    }
}

• FastReader

  백준 자바 입출력 템플릿

DP를 사용하는 문제 리스트

• 2839 - 설탕 배달 (실버 4)
• 1003 - 피보나치 함수 (실버 3)
• 2579 - 계단 오르기 (실버 3)
• 9461 - 파도반 수열 (실버 3)
• 12865 - 평범한 배낭 (골드 5)
• 2293 - 동전 1 (골드 5)
• 11054 - 가장 긴 바이토닉 부분 수열 (골드 4)

누군가가 물어본다면

DP는 하위 문제의 결과를 재사용하여 전체 문제의 결과를 효율적으로 구할 수 있는 기법입니다.