이진 탐색 트리 BST(Binary Search Tree)

Posted Apr 22, 2024

By ROOT

15 min read

🤔 BST 란?

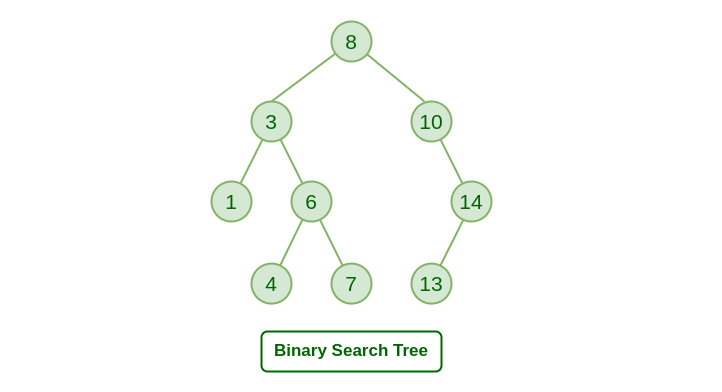
이진 트리 기반의 탐색을 위한 자료구조이다.
노드의 왼쪽 자식은 부모의 값보다 작은 값을 가져야 하며 노드의 오른쪽 자식은 부모의 값보다 큰 값을 가져야 한다.

[이진 탐색 + 연결 리스트]

이진 탐색
- 탐색에 소요되는 시간 복잡도는 O(log n)
- 하지만 삽입, 삭제가 불가능하다.
연결 리스트
- 삽입, 삭제의 시간 복잡도는 O(1)
- 하지만 탐색하는 시간 복잡도는 O(n)
두 자료구조의 장점만을 가져오기 고안된 것이 이진 탐색 트리 이다.
즉, 효율적인 탐색 능력을 가지고 자료이 삽입, 삭제도 가능하게 만드는 것이다.

😄 특징

이진 트리의 일종으로 이진 탐색 트리에는 데이터를 저장하는 규칙이 있다.
이진 탐색 트리의 노드에 저장된 키는 유일하다. 즉, 중복이 없다.
이진 탐색 트리의 순회는 중위 순회(in order) 방식이다.(왼쪽 - 부모 - 오른쪽)
중위 순회로 정렬된 순서를 읽을 수 있다.

[시간 복잡도]

탐색
- 균일한 일반적인 트리 : O(log n)
- 편향 트리 : O(n)
삽입, 검색, 삭제의 시간 복잡도는 트리의 depth에 비례한다.

🥸 BST 핵심 연산

삽입
삭제
검색
트리 생성
트리 삭제

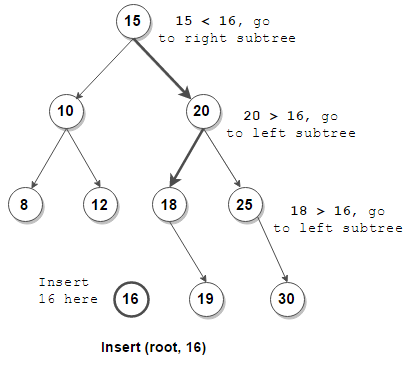
[삽입]

루트 노드부터 탐색을 시작한다.

현재 탐색 노드와 삽입하려는 노드의 크기를 비교한다.
현재 탐색 노드보다 작다면 왼쪽 자식 노드로, 크다면 오른쪽 자식 노드로 탐색 노드를 변경한다.
현재 탐색 노드가 null일 때까지 1~2 를 반복한다.
현재 탐색 노드가 null이면 해당 자리에 노드를 생성하고, 부모와의 자식 관계를 설정한다.

[삭제]

3가지 경우로 나누어 살펴봐야한다.

삭제하는 노드가 자식노드를 갖고 있지 않을 때
- 해당 노드만 삭제하면 된다.
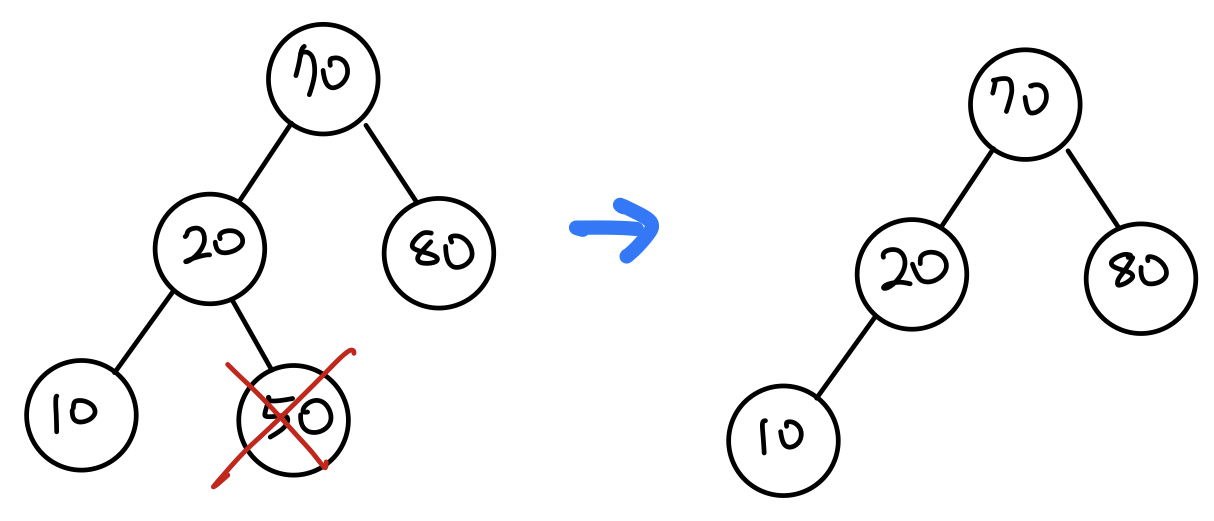
삭제하는 노드가 하나의 자식노드를 갖고 있을 때
- 삭제한 노드 위치에 자식 노드를 넣으면 된다.
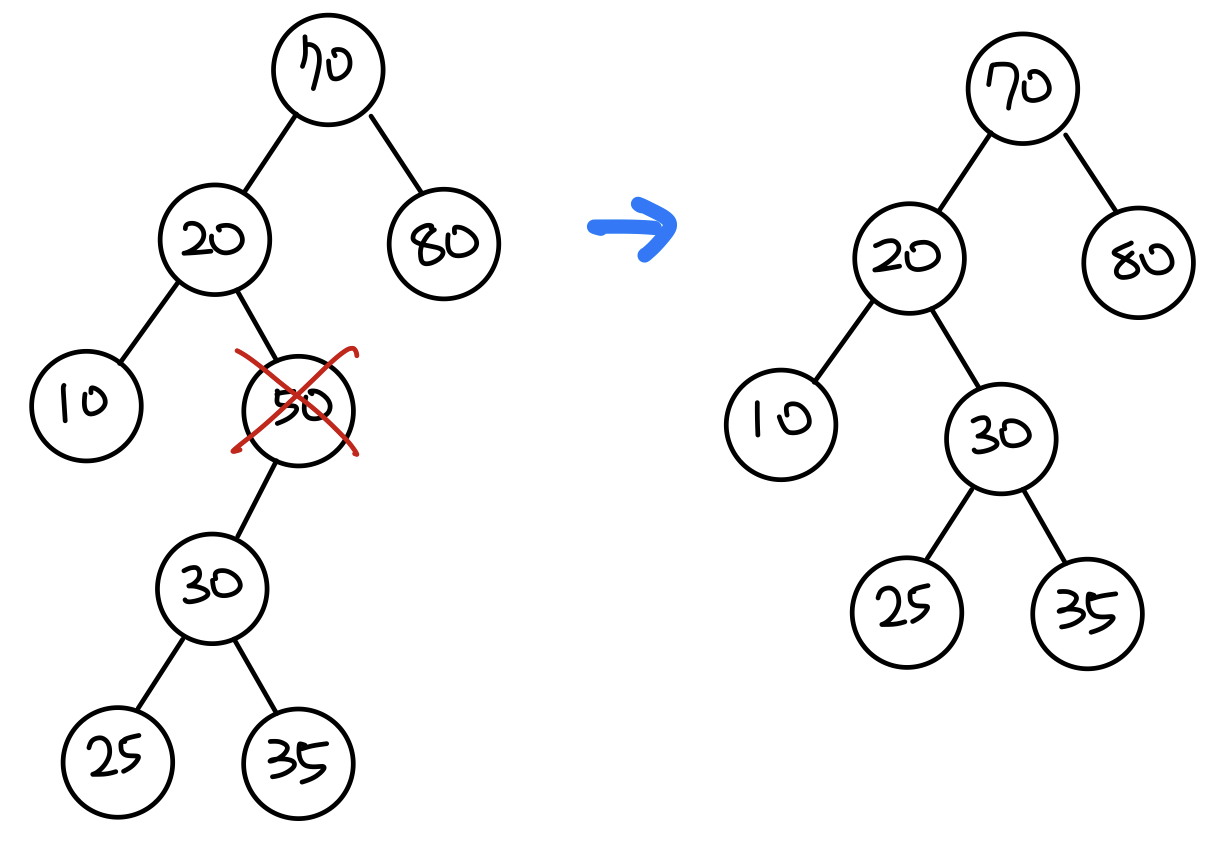
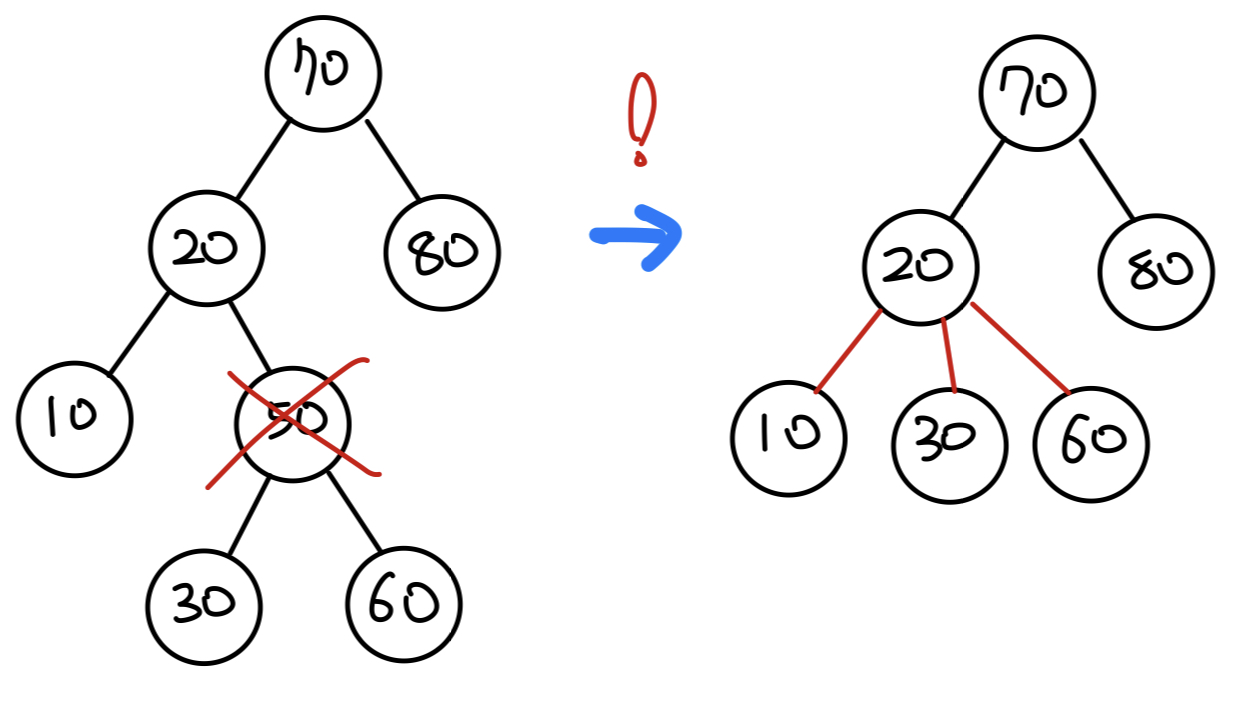
삭제하는 노드가 두 개의 자식 노드를 갖고 있을 때
- 2번 처럼 그냥 자식노드를 넣어버리면 자식노드가 3개가 되므로 이진 트리의 조건을 만족하지 않게 된다.
- 다음 2가지 방법을 사용할 수 있다.
  1. 삭제된 노드의 오른쪽 자식노드에서 제일 작은 노드로 대체한다.
  2. 삭제된 노드의 왼쪽 자식노드에서 제일 큰 노드로 대체한다.
- 1번 예시
- 이 방법이 가능한 이유는 1번의 경우 50 < x < 70 이고, 2번의 경우 20 < y < 50 이기 때문이다.

[검색]

검색은 삽입과 비슷하다.
루트 노드부터 탐색을 시작한다.

현재 탐색 노드와 찾는 노드의 크기를 비교한다.
현재 탐색 노드보다 작다면 왼쪽 자식 노드로, 크다면 오른쪽 자식 노드로 탐색 노드를 변경한다.
현재 탐색 노드가 null이거나 같은 값을 찾을 때까지 1~2 를 반복한다.
현재 탐색 노드가 null이라면 찾는 노드는 없다는 것을 뜻하고(false), 같은 값이 있다면 찾는 노드가 있다는 뜻이다.(true)

😭 자바로 구현해보기

보통 트리에는 size까지 설정을 하지만, 여기서는 삽입, 삭제, 검색 기능에 초점을 맞춰서 간단하게 알아보겠다.
삽입, 삭제, 검색은 재귀로 구현된다.

[Node class]

연결리스트와 유사하게 BST에서의 각 노드는 키값을 가지고 왼쪽 자식노드와 오른쪽 자식노드를 참조한다.

  
class Node {
    int key;
    Node left, right;

    public Node(int key) {
        this.key = key;
        left = right = null;
    }
}

[BinarySearchTree class]

기본적인 BST 클래스의 구성은 다음과 같다.
삽입, 삭제, 검색을 차례로 알아보고, 추가로 중위 순회임을 이용해 트리의 원소들을 오름차순 정렬로 출력하는 순회 메서드를 만들어보겠다.

  
class BinarySearchTree {
    Node root;

    BinerySearchTree() {    // 처음 생성 시 원소가 없음
        root = null;
    }

    // 삽입 메서드

    // 삭제 메서드

    // 검색 메서드

    // 순회 메서드(오름차순 정렬로 출력)
}

[insert]

루트 노드부터 재귀적으로 탐색을 시작하여 가장 하위 트리부터 순차적으로 업데이트한다.

  
void insert(int key) {
    // 루트 노드부터 탐색 시작
    root = insertRecursive(root, key);
}

Node insertRecursive(Node now, int key) {
    if (now == null) {  // 현재 탐색하는 노드가 null 이라면 해당 자리에 노드 삽입
        return new Node(key);
    }

    if (key < now.key) {    // 현재 탐색하는 노드값이 삽입하는 노드값보다 작은 경우
        now.left = insertRecursive(now.left, key);  // 왼쪽 자식노드 탐색
    } else if (key > now.key) { // 현재 탐색하는 노드값이 삽입하는 노드값보다 큰 경우
        now.right = insertRecursive(now.right, key);    // 오른쪽 자식노드 탐색
    }

    return now;
}

[delete]

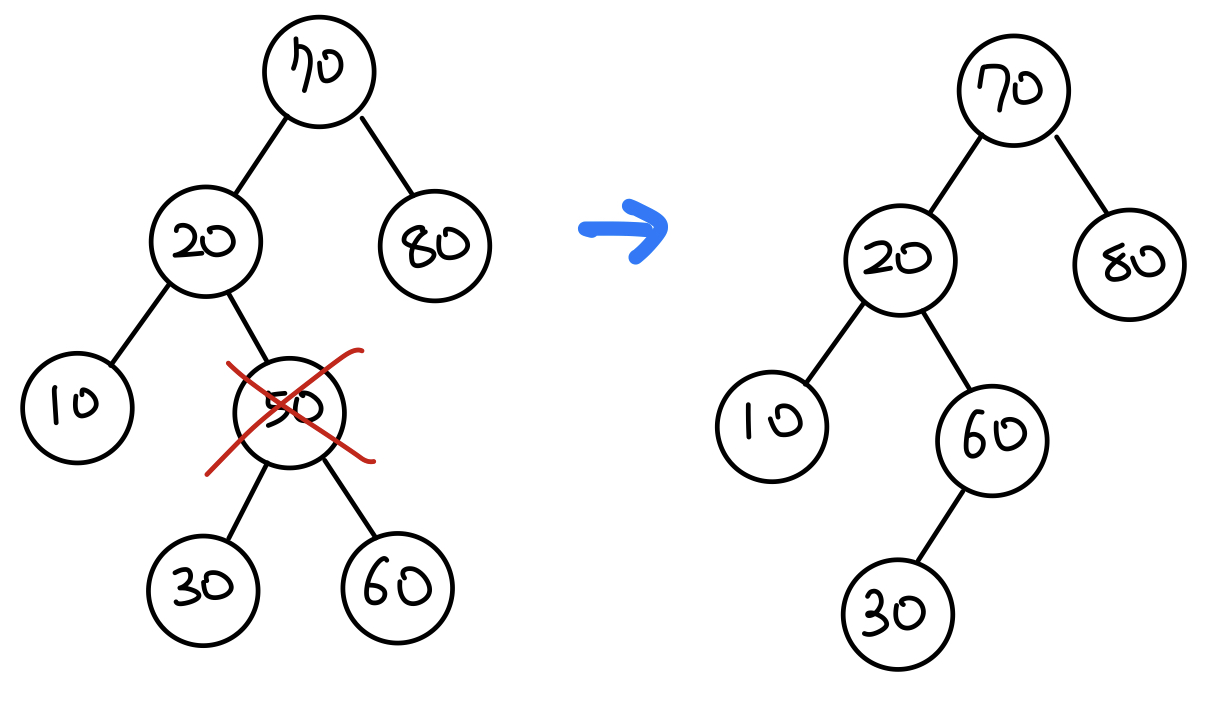
위에서 언급했던 자식 노드가 2개일 때의 삭제 방법 중 삭제된 노드의 오른쪽 자식노드에서 제일 작은 노드로 대체하는 방법을 사용했다.
이에 따라 트리에서 최솟값을 찾는 minValue 메서드도 추가했다.
now.right = deleteRecursive(now.right, now.key);
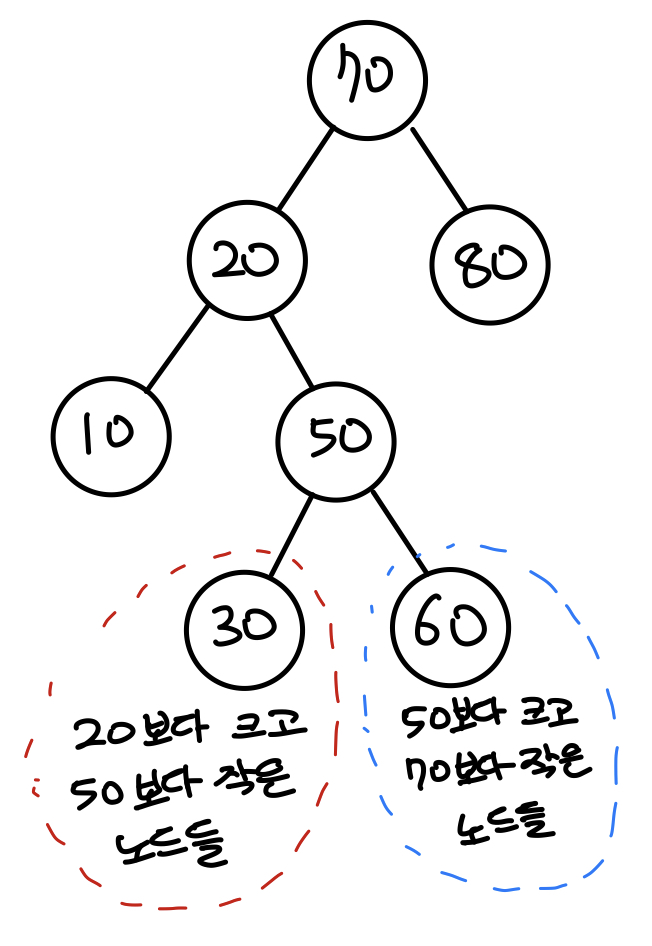
- 위 코드에서 똑같이 자식노드가 2개면 어떡하지? 라는 생각을 할 수 있지만 자식노드는 많아야 1개이다.
- 정확하게는 왼쪽 자식 노드는 존재할 수 없다.
- 이 노드는 최솟값인데 왼쪽 자식 노드가 있다면 최솟값은 왼쪽 자식 노드가 될 것이다.

  
void deleteKey(int key) {
    // 루트 노드부터 탐색 시작
    root = deleteRecursive(root, key);
}

Node deleteRecursive(Node now, int key) {
    if (now == null)    // 현재 탐색하는 노드가 null이라면 삭제하려는 키값을 가진 노드가 존재하지 않다는 것
        return now;
        
    if (key < now.key)
        now.left = deleteRecursive(now.left, key);  // 왼쪽 자식노드 탐색
    else if (key > now.key)
        now.right = deleteRecursive(now.right, key);    // 오른쪽 자식노드 탐색
    else {  // 삭제하려는 키값을 가진 노드를 찾았을 때
        // 1. 자식노드가 없다면 null 로 설정
        // 2. 자식노드가 하나라면 삭제된 노드자리에 해당 자식노드 삽입
        if (now.left == null)
            return now.right;
        else if (now.right == null)
            return now.left;
        
        // 3. 자식노드가 2개라면

        // 오른쪽 자식 노드의 최솟값을 현재 키값으로 설정하고
        now.key = minValue(now.right);

        // 해당 노드를 삭제한 뒤 업데이트
        // 이때, 이 노드는 최솟값을 가진 노드이므로 이 노드의 자식노드는 많아야 1개다.
        now.right = deleteRecursive(now.right, now.key);
    }

    return now;
}

int minValue(Node now){
    int minv = now.key;
    while (now.left != null) {
        minv = now.left.key;
        now = now.left;
    }
    return minv;
}

[search]

찾는 값이 트리에 존재하는지의 여부를 true or false 로 알려준다.

  
boolean search(int key) {
    // 루트 노드부터 탐색 시작
    return searchRecursive(root, key);
}

boolean searchRecursive(Node now, int key) {
    if (now == null) // 현재 탐색 노드가 null 이라면 트리에 존재하지 않는것 -> false
        return false;
        
    if (now.key == key) // 현재 탐색 노드의 키값이 찾으려는 값과 같다면 존재하는 것 -> true
        return true;
    
    // 키값의 크기 비교를 통해 왼쪽 또는 오른쪽 자식노드를 탐색
    return key < now.key ? searchRecursive(now.left, key) : searchRecursive(now.right, key);
}

[inorder print]

출력 순서 : 왼쪽 자식 노드 - 자신 - 오른쪽 자식 노드

  
void inorder() {
    inorderRecursive(root);
}

void inorderRecursive(Node now) {
    if (now != null) {
        inorderRecursive(now.left); // 왼쪽 자식 노드 먼저 출력
        System.out.print(now.key + " ");
        inorderRecursive(now.right);    // 오른쪽 자식 노드는 가장 마지막에 출력
    }
}

[전체 코드]

  
class Node {
    int key;
    Node left, right;

    public Node(int key) {
        this.key = key;
        left = right = null;
    }
}

class BinarySearchTree {
    Node root;

    BinarySearchTree() {
        root = null;
    }

    void insert(int key) {
        root = insertRecursive(root, key);
    }

    Node insertRecursive(Node now, int key) {
        if (now == null) {
            return new Node(key);
        }

        if (key < now.key) {
            now.left = insertRecursive(now.left, key);
        } else if (key > now.key) {
            now.right = insertRecursive(now.right, key);
        }

        return now;
    }

    void deleteKey(int key) {
        root = deleteRecursive(root, key);
    }

    Node deleteRecursive(Node now, int key) {
        if (now == null)
            return now;
        
        if (key < now.key)
            now.left = deleteRecursive(now.left, key);
        else if (key > now.key)
            now.right = deleteRecursive(now.right, key);
        else {
            if (now.left == null)
                return now.right;
            else if (now.right == null)
                return now.left;
            
            now.key = minValue(now.right);

            now.right = deleteRecursive(now.right, now.key);
        }

        return now;
    }

    int minValue(Node now){
        int minv = now.key;
        while (now.left != null) {
            minv = now.left.key;
            now = now.left;
        }
        return minv;
    }

    boolean search(int key) {
        return searchRecursive(root, key);
    }

    boolean searchRecursive(Node now, int key) {
        if (now == null)
            return false;
        
        if (now.key == key)
            return true;
        
        return key < now.key ? searchRecursive(now.left, key) : searchRecursive(now.right, key);
    }

    void inorder() {
        inorderRecursive(root);
    }

    void inorderRecursive(Node now) {
        if (now != null) {
            inorderRecursive(now.left);
            System.out.print(now.key + " ");
            inorderRecursive(now.right);
        }
    }
}

public class Main {
    public static void main(String[] args) {
        BinarySearchTree bst = new BinarySearchTree();

        bst.insert(70);
        bst.insert(20);
        bst.insert(50);
        bst.insert(30);
        bst.insert(10);
        bst.insert(60);
        bst.insert(40);
        bst.insert(80);

        System.out.println("원본");
        bst.inorder();

        bst.deleteKey(20);
        bst.deleteKey(30);
        bst.deleteKey(50);
        bst.deleteKey(950);

        System.out.println();
        System.out.println("-----------");

        System.out.println("삭제 작업 후 트리");
        bst.inorder();

        // 출력
        /**
        원본
        10 20 30 40 50 60 70 80 
        -----------
        삭제 작업 후 트리
        10 40 60 70 80
        **/
    }
}

누군가가 물어본다면

이진 탐색 트리는 이진 탐색과 연결 리스트의 장점만을 갖기 위해 고안된 자료구조입니다.

탐색은 일반적으로 O(log n) 이지만, 편향 트리인 경우 O(n)이 됩니다. 삽입, 삭제, 검색 연산은 트리의 depth에 비례합니다.

data structure

data structure binary search tree

This post is licensed under CC BY 4.0 by the author.