b+ tree 개념과 삽입, 삭제 알아보기

🙃 B+ 트리 (B+ Tree)

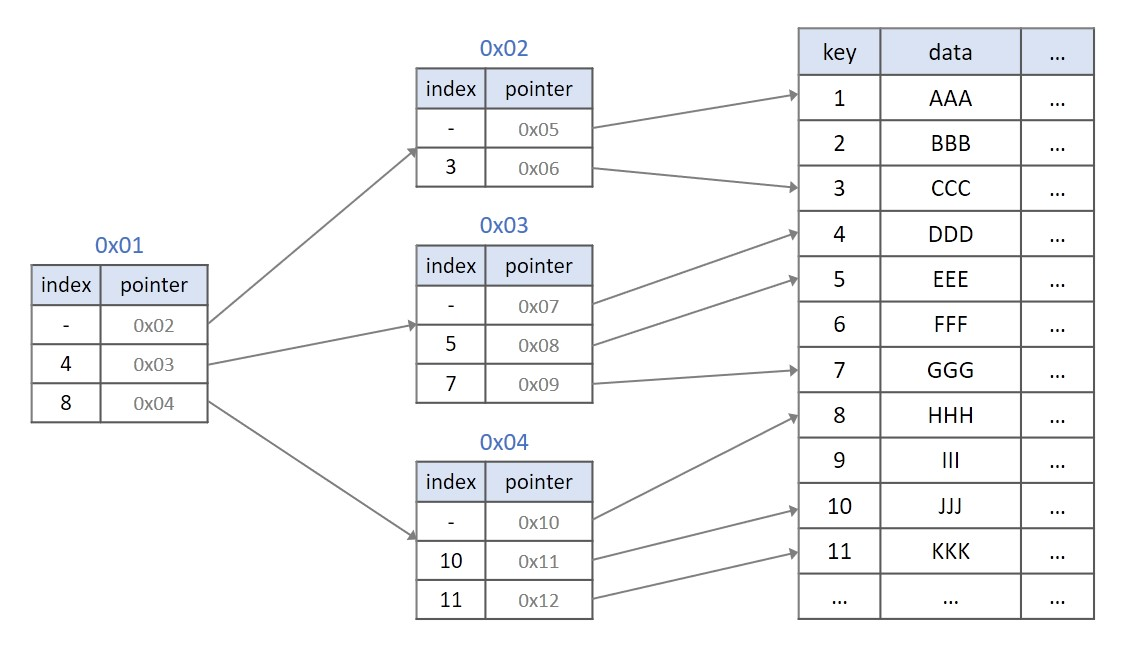
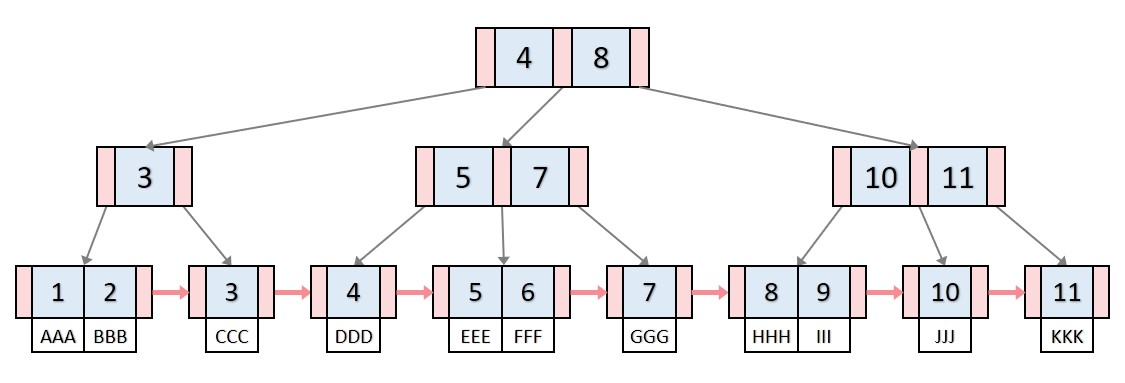
• 기존의 B-Tree와 데이터의 연결리스트로 구현된 색인구조다.
• b-tree 와의 가장 큰 차이점은 리프노드가 아닌 노드(Internal Node)에 데이터가 아닌 주소(인덱스)가 들어가있다는 것이다.
• 데이터들은 리프노드에만 들어있다.

[장점]

• internal node에서 데이터를 저장하지 않으므로 블럭 사이즈를 더 많이 이용할 수 있다.

  b tree의 internal node : 데이터 + 자식 노드 포인터, b+ tree의 internal node : 자식 노드 포인터

• 리프노드끼리 연결 리스트로 연결되어 있어서 순차 탐색과 범위 탐색에 매우 유리하다.

[단점]

• b tree는 최상 케이스의 경우 루트 노드에서 끝나 O(1) 이 될 수 있지만 b+ tree는 무조건 리프노드까지 내려가봐야 한다.

🥱 데이터 삽입

기본적으로 b tree와 비슷한 로직이다.

• 추가는 항상 리프 노드에 한다.
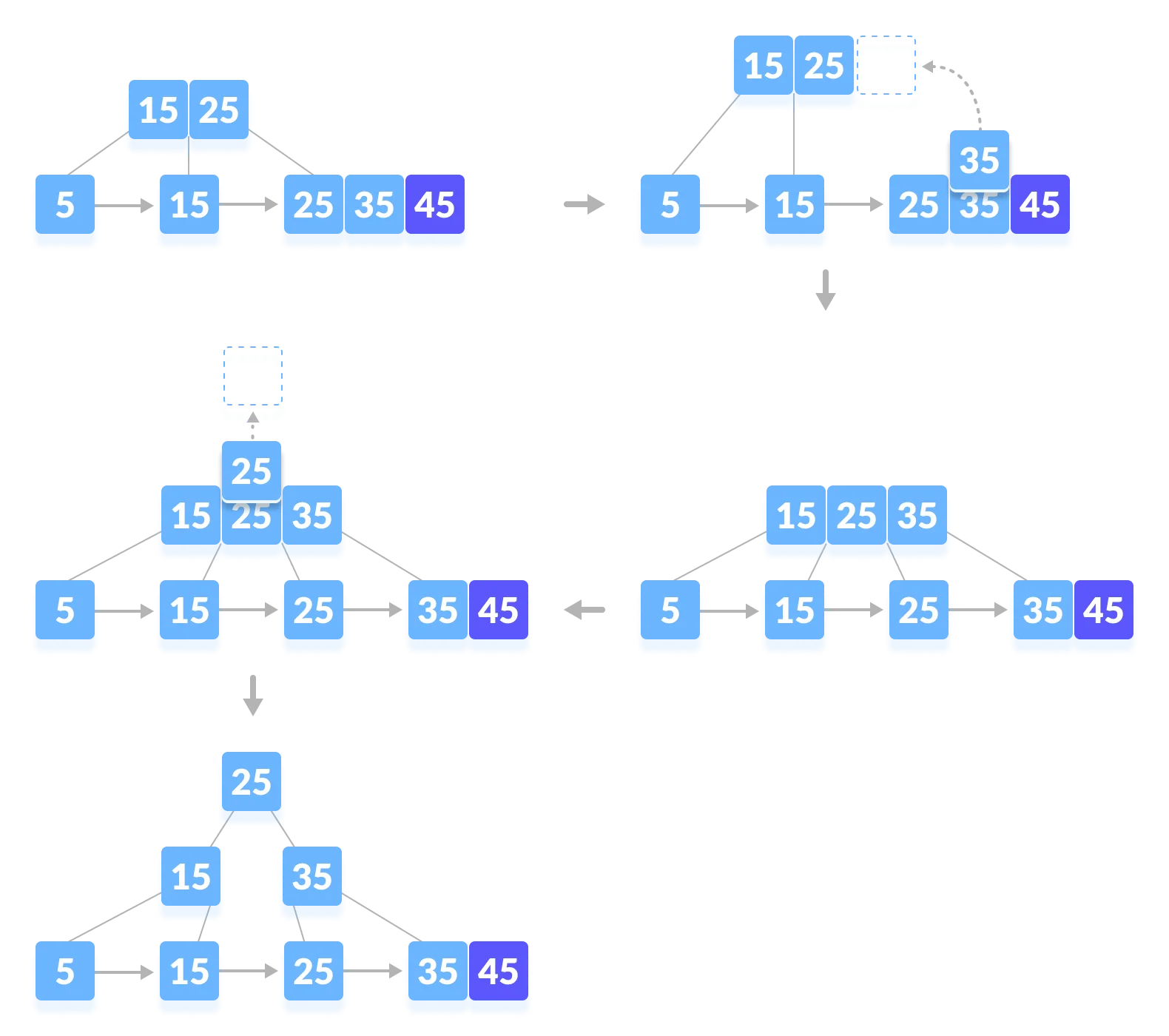
• 노드가 넘치면 가운데 key를 기준으로 좌우 key들을 분할하고 가운데 key는 승진한다.
  • b+ tree 추가
    • 이때 기존에 있던 가운데 key는 오른쪽으로 붙는다.
    • 결과적으로 승진한 key가 가리키는 오른쪽 자식노드의 첫번째가 진짜 데이터가 들어있는 가운데 key가 된다.

[데이터 삽입 예시]

• 차수 : 3
• 45을 삽입했을 때 연쇄적으로 분할이 일어나는 예시

😴 데이터 삭제

삭제도 마찬가지로 데이터 삭제 후 b+ tree 조건에 맞는지 확인하고 재조정하는 단계를 거친다.

[b+ tree 조건]

• M : 최대 자식 수(차수)
• 노드는 최대 M개의 자식을 가질 수 있다.
• 노드는 최대 M-1개의 key를 가질 수 있다.
• 노드에는 최소 M/2개의 자식 노드가 있어야 한다.
• 루트를 제외한 노드에는 최소 M/2 - 1 개의 key가 있어야 한다.
• 삭제한 키의 인덱스가 internal node에 존재한다면 해당 노드도 삭제해야 한다.

[데이터 삭제 예시]

• 차수 : 3
• 삭제할 대상의 인덱스가 없는 경우(internal node 에 없는 경우)와 있는 경우, 높이가 낮아지는 경우를 알아보자

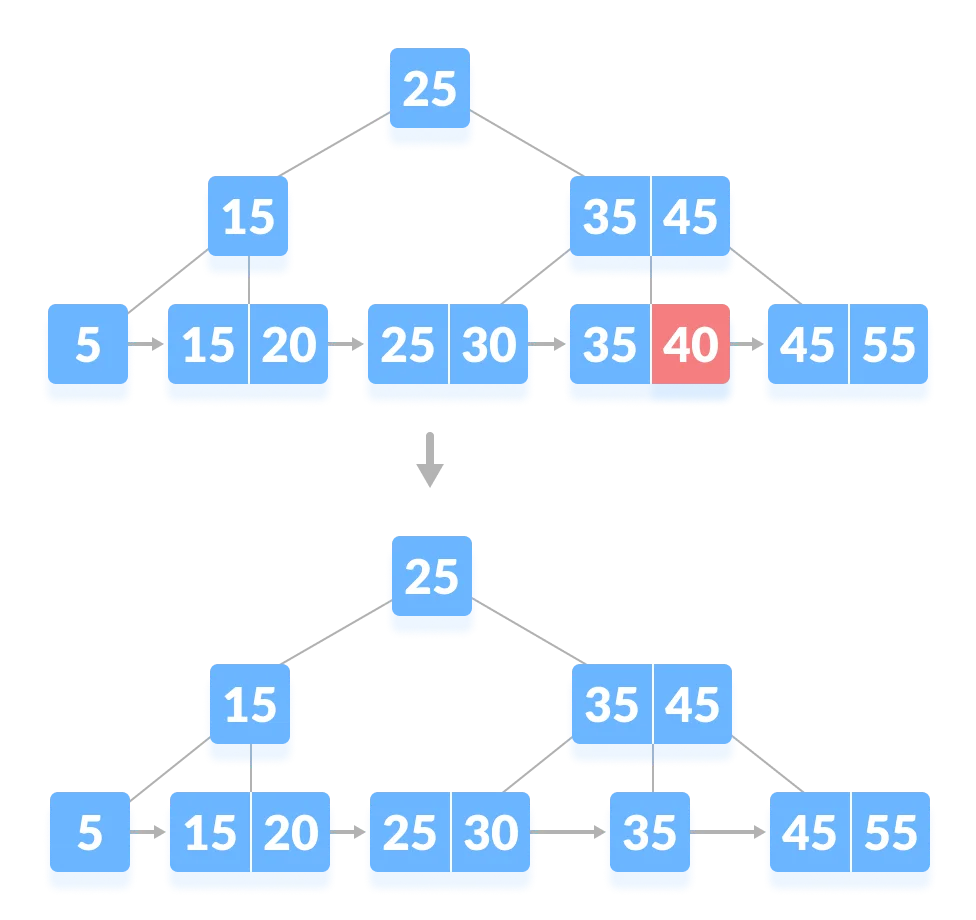
1-1. 인덱스도 없고 재조정도 필요 없는 경우

• 40 삭제
• 삭제 후에도 최소 개수 조건을 만족하므로 재조정이 일어나지 않는다.

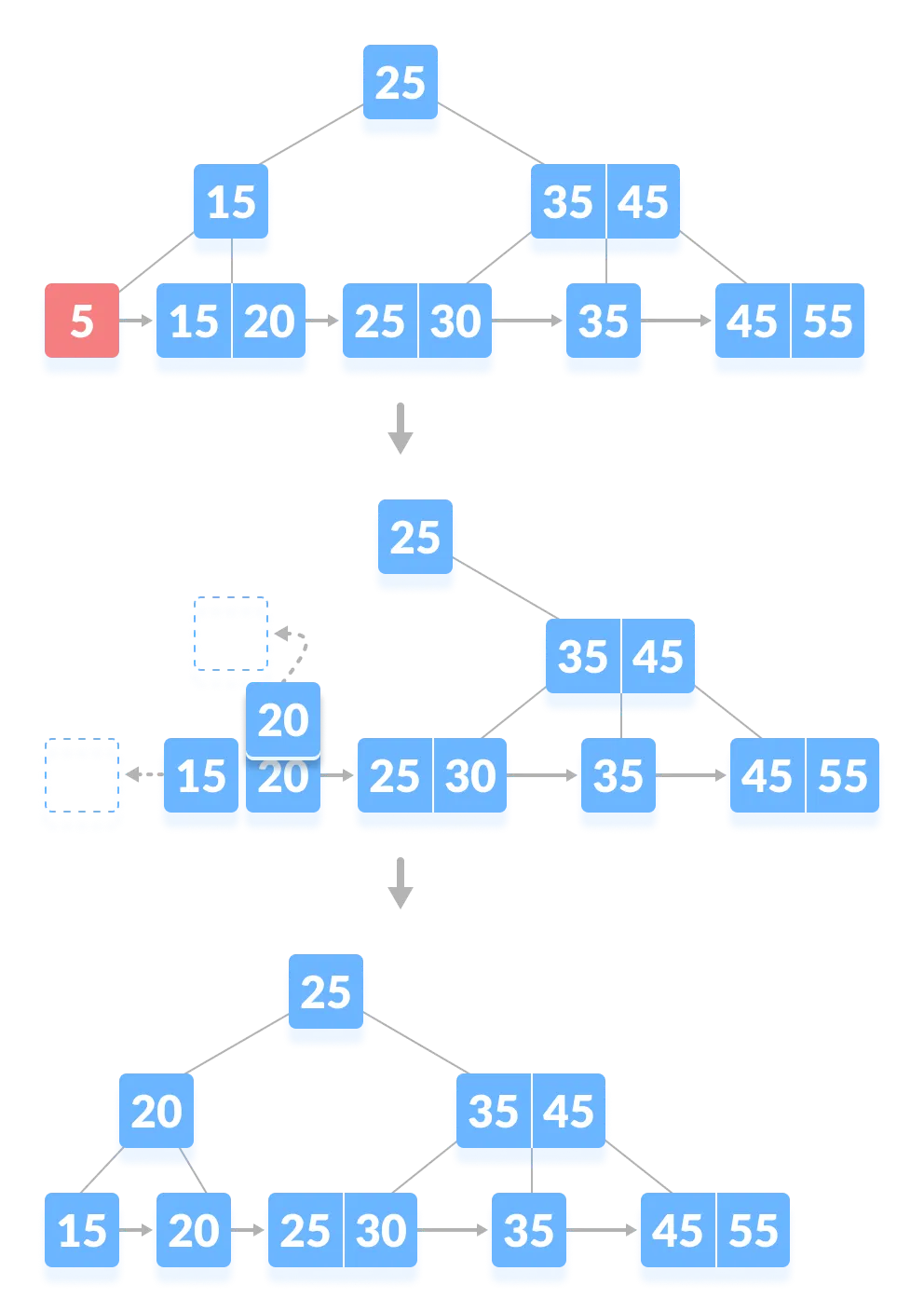
1-2. 인덱스는 없지만 재조정이 필요한 경우

• 5 삭제
• 최소 개수 조건을 만족하지 않으므로 재조정이 일어난다.
• 형제 노드로부터 데이터를 빌리고 조건에 맞게 인덱스도 업데이트 해준다.

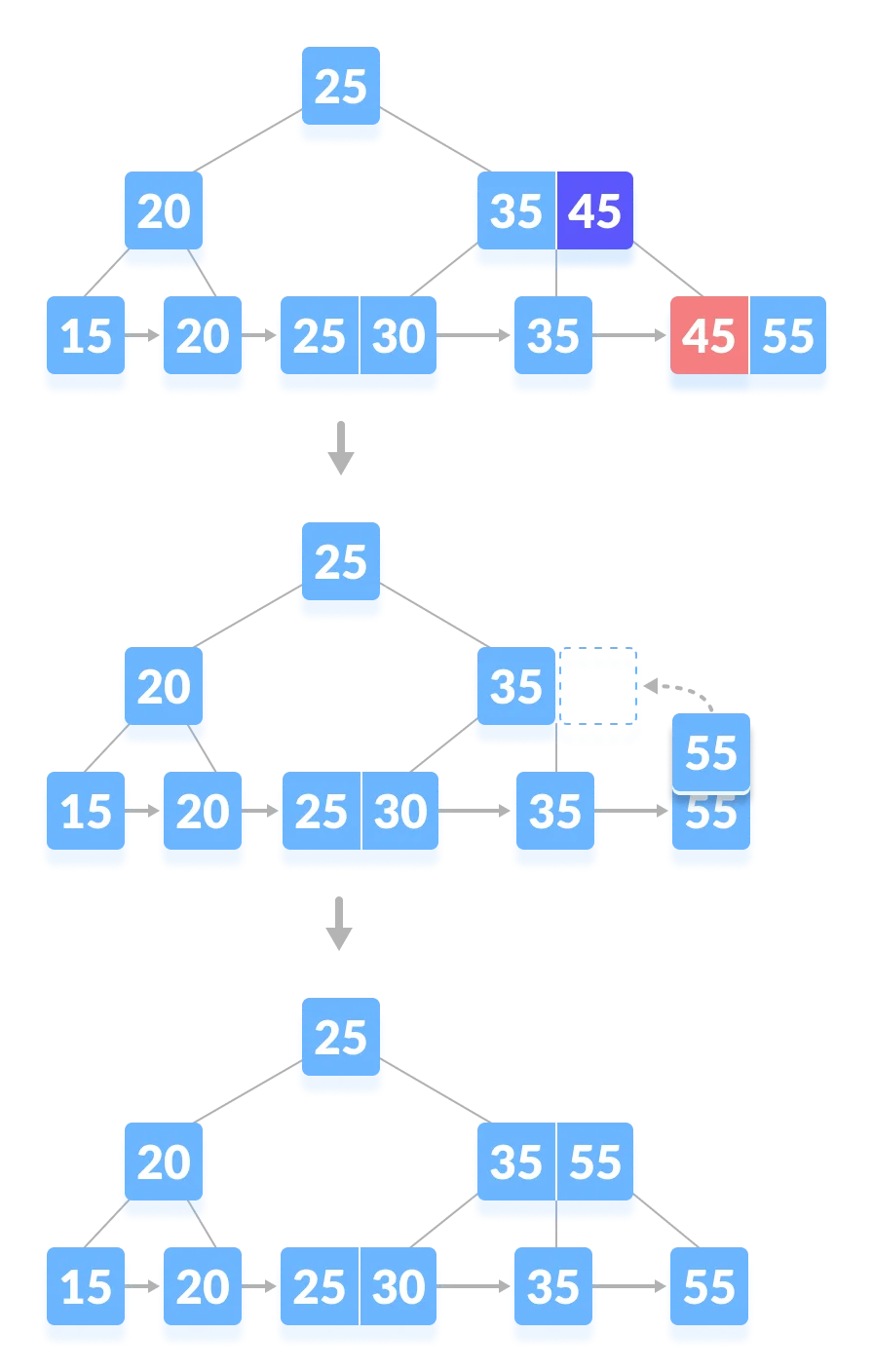
2-1. (삭제할 대상의) 인덱스가 있고 삭제 후 최소 개수가 만족되는 경우

• 45 삭제
• 최소 개수가 만족되므로 재조정은 필요하지 않다.
• 삭제된 인덱스 대신 같은 노드 안에 있던 key를 인덱싱한다.

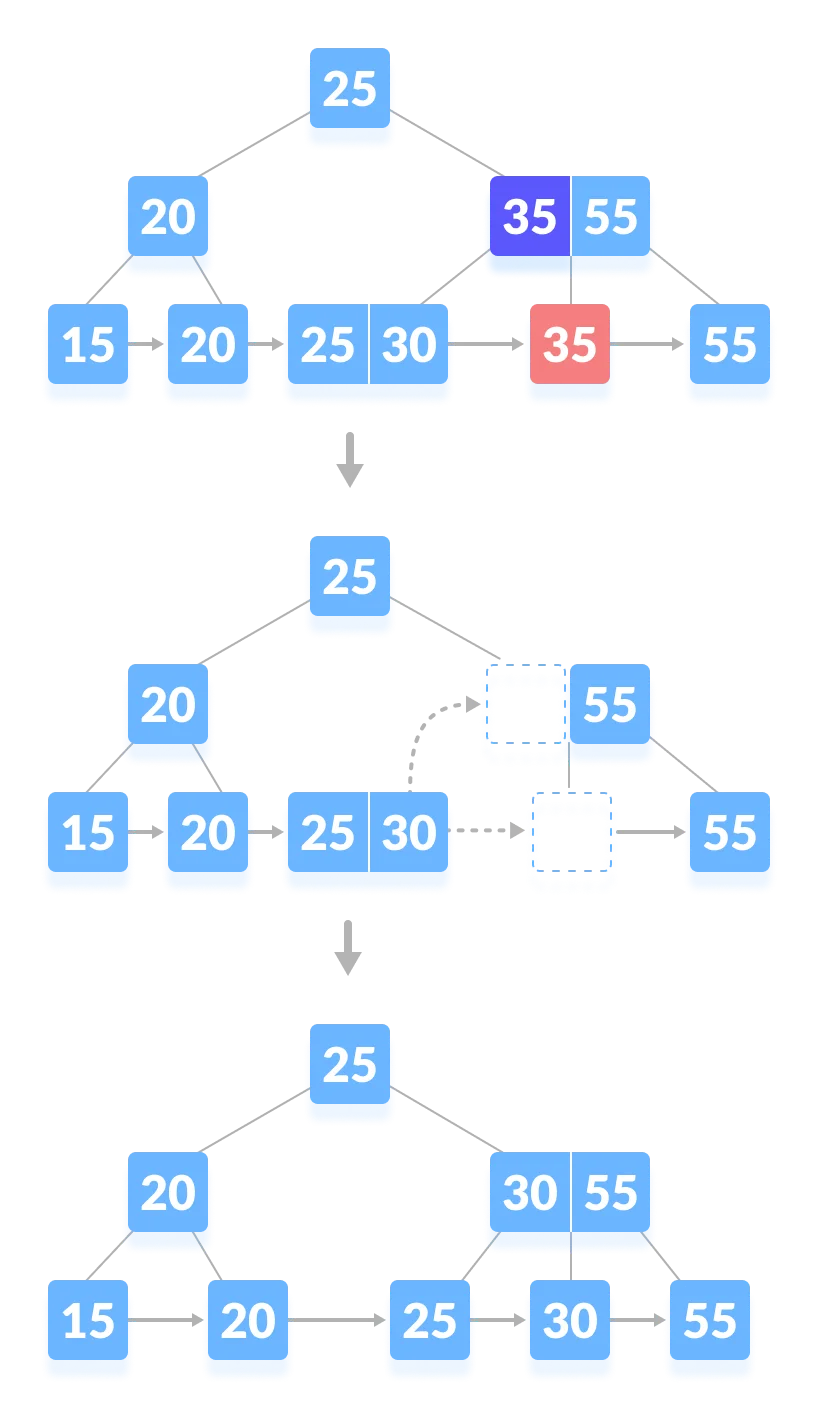
2-2. 인덱스가 있고 삭제 후 최소 개수가 만족되지 않는 경우

• 35 삭제
• 재조정이 일어나 형제 노드로부터 데이터를 빌린다.
• 삭제된 인덱스에는 빌린 데이터의 key를 인덱싱한다.

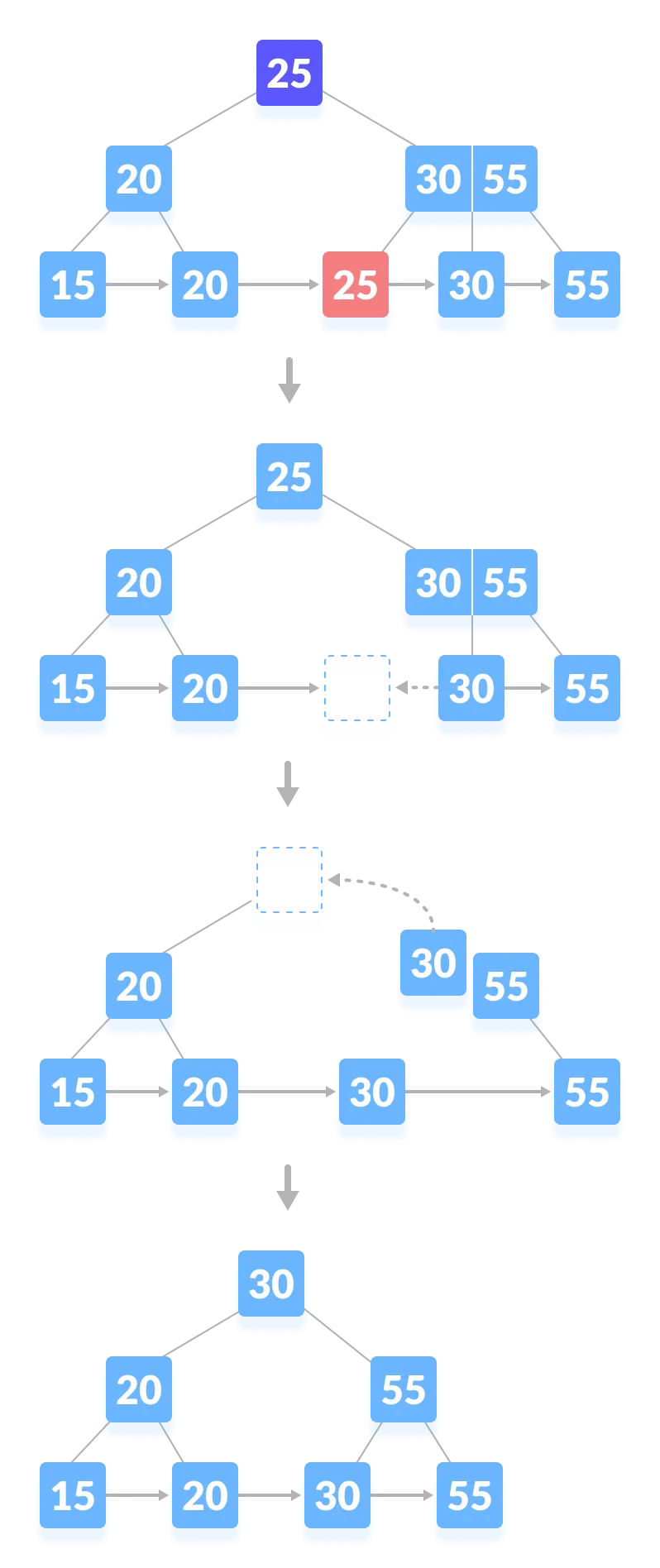
2-3. 인덱스가 조상 노드(부모의 부모)에 있고 최소 개수가 만족되지 않는 경우

• 25 삭제
• 리프 노드에서는 형제도 충분한 개수를 가지고 있지 않으므로 병합한다.
• 삭제된 인덱스에는 중위 계승자(병합한 형제 노드)로 대체한다.

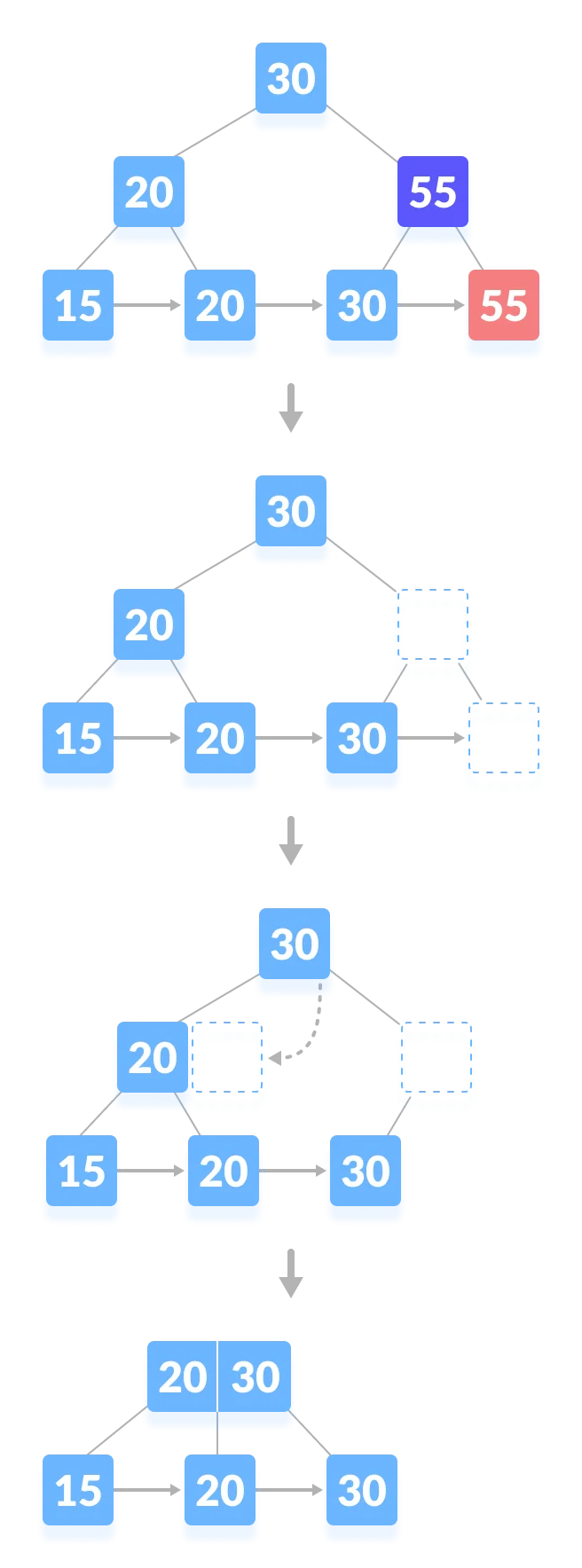
3-1. 트리의 높이가 줄어드는 복잡한 경우

• 55 삭제

1. 55 key와 인덱스 삭제
2. 리프 노드의 재조정
   1. 형제 노드로부터 데이터를 빌릴 수 있는지 확인
   2. 빌릴 수 없으므로 형제 노드와 병합
3. 인덱싱 재조정
   1. 형제 노드로부터 인덱스를 빌릴 수 있는지 확인
   2. 빌릴 수 없으므로 부모 노드로부터 빌릴 수 있는지 확인
   3. 빌릴 수 없으므로 부모와 형제를 병합

누군가가 물어본다면

B+ Tree는 리프노드에만 데이터를 저장하여 internal node 공간을 효율적으로 사용할 수 있지만 탐색을 위해 무조건 리프노드까지 가야한다는 단점이 있습니다.

리프노드끼리 연결 리스트로 연결되어 있어 B Tree 보다 순차 탐색과 범위 탐색에 유리합니다.