이진 탐색(Binary Search)

Binary Search 란?

• 이진 탐색 / 이분 탐색 이라고 부른다.
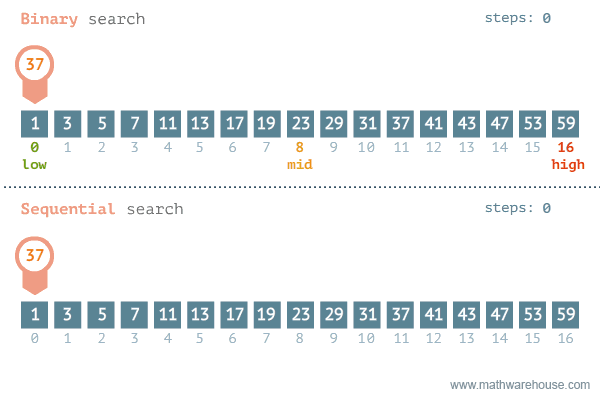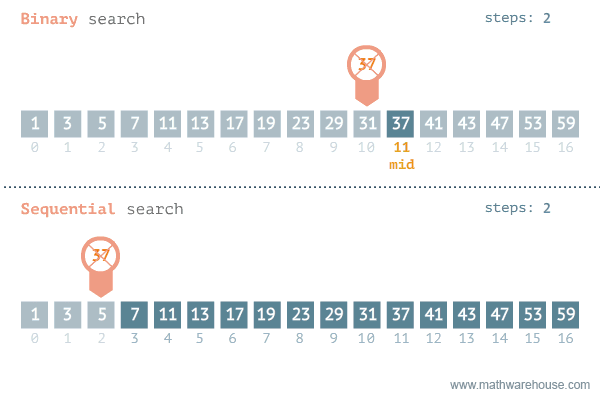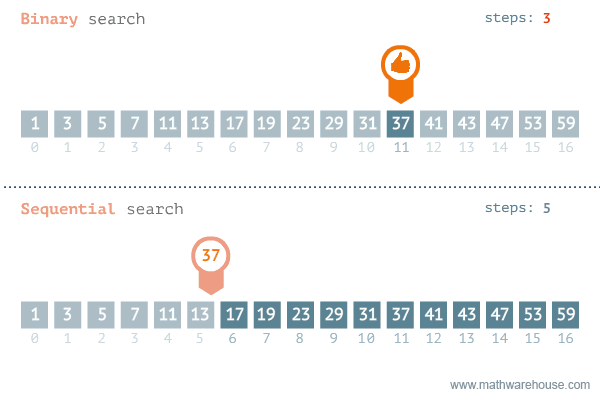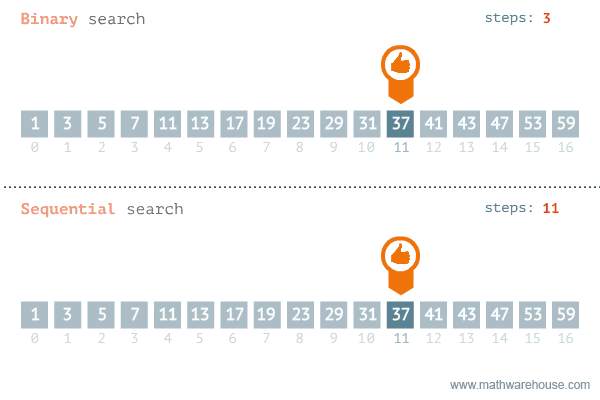
• 정렬되어 있는 리스트 에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법이다.
• 배열 내부가 정렬되어 있어야만 사용할 수 있는 알고리즘이다.
• 변수 3개(start, end, mid) 를 사용하여 탐색한다.
• 최악의 경우 순차 탐색의 경우 O(n) 걸리는 반면, 이진 탐색은 O(log n) 이걸린다.
• 효과적인 성능으로 대부분의 코테 문제에서 성능을 향상시키는 방법으로 주로 사용한다.

BOJ 1920 - 수 찾기 (실버 4)

1920-수 찾기

• N개의 정수들과 M개의 정수들이 각각 주어진다.

  N개의 정수들을 A, M개의 정수들을 B라고 하겠다.

• B의 각 정수들이 A에 존재하는지 알아내야 한다.

• 있는 경우 1, 없는 경우 0을 출력한다.

• B의 각 정수들에 대해 이분 탐색을 수행한다.

import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
    static FastReader scan = new FastReader();

    static StringBuilder sb = new StringBuilder();

    static int n, m;
    static int[] arr;

    public static void main(String[] args) {
        input();
        System.out.println(sb.toString());
    }
    static void input(){
        n = scan.nextInt();

        arr = new int[n];
        for (int i=0;i<n;i++){
            arr[i] = scan.nextInt();
        }

        Arrays.sort(arr);

        m = scan.nextInt();
        for (int i=0;i<m;i++){
            solve(scan.nextInt());
        }
    }
    static void solve(int x){
        int start = 0;
        int end = n-1;
        int result = 0;
        while(start<=end){
            int mid = (start+end)/2;

            if (x==arr[mid]){
                result = 1;
                break;
            }else if (x<arr[mid]){
                end = mid-1;
            }else {
                start = mid+1;
            }
        }
        if (sb.length()>0){
            sb.append("\n");
        }
        sb.append(result);
    }
    static class FastReader {
        // 생략
    }
}

• FastReader

  백준 자바 입출력 템플릿

이분 탐색을 사용하는 문제 리스트

• 10816-숫자 카드 2 (실버 4)
• 1654-랜선 자르기 (실버 2)
• 2805-나무 자르기 (실버 2)
• 2343-기타 레슨 (실버 1)

이진 탐색 자체가 어려운 개념은 아니기에 순수한 이진 탐색 문제의 난이도는 실버 정도다. 보통 다른 개념들과 합쳐져서 성능 향상 목적으로 자주 쓰이니 위 문제들로 이분 탐색 개념을 잡는 것이 중요하다.

누군가가 물어본다면

이진 탐색은 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법입니다.
효과적인 성능으로 다른 개념들과 합쳐져서 코테 문제에 사용됩니다.