Post

Union-Find Algorithm (유니온-파인드)

Posted
By ROOT
6 min read

🤔 유니온 파인드 알고리즘이란?

  • 상호 배타적 집합, Disjoin-set(서로소 집합) 이라고도 부른다.
  • 최종 목표는 합연산을 진행하면서, 어떤 두 노드가 같은 집합에 있는지 확인하는 것이다.
  • 이 알고리즘은 Union과 Find 두가지의 연산을 진행한다.
  • 크루스칼 알고리즘과 프림 알고리즘에 사용된다.


😮 Find 연산

  • 하나의 원소가 어떤 집합에 속해있는지를 판단한다.
  • Find 연산은 인자로 들어온 원소의 루트 노드를 반환한다.


😮 Union 연산

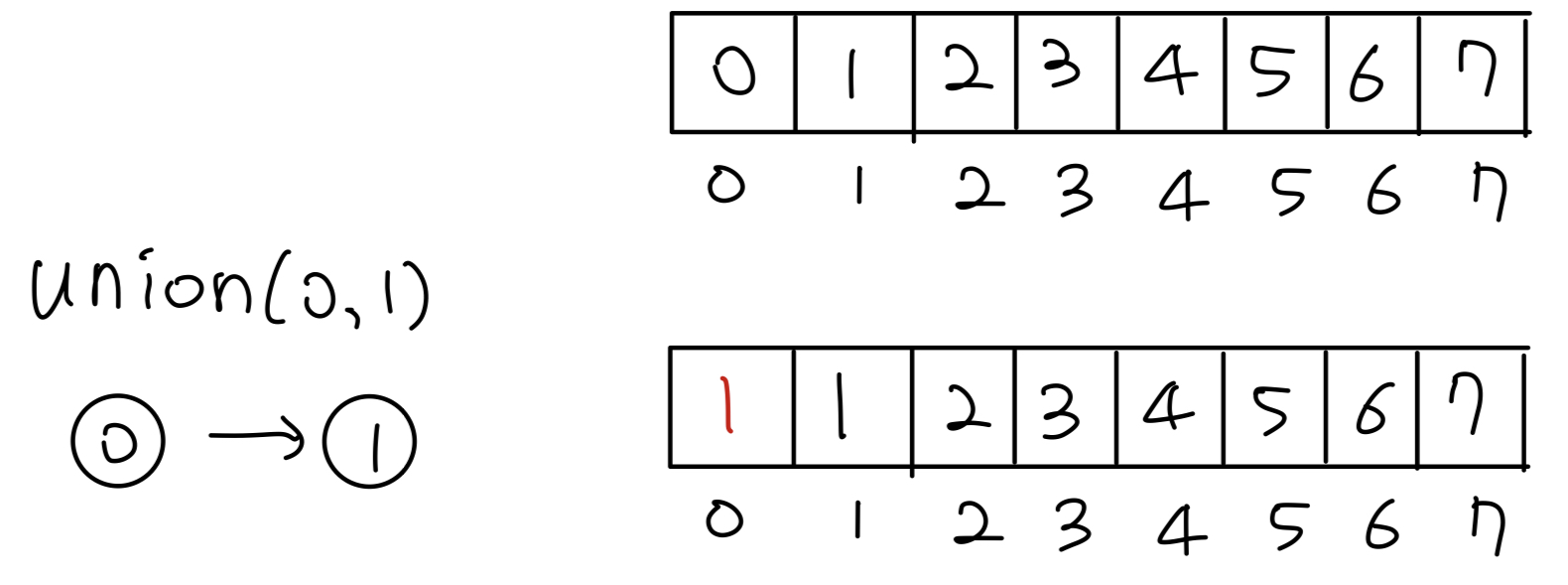
  • 서로 다른 두개의 집합을 하나의 집합으로 병합하는 연산
  • 합집합 연산과 같다.


😤 로직 알아보기

  • 기본적으로 배열을 사용하여 문제를 풀어나간다.
  • 각 원소들은 배열의 인덱스가 되고 값으로는 자신이 가리키는 부모 인덱스를 저장한다.
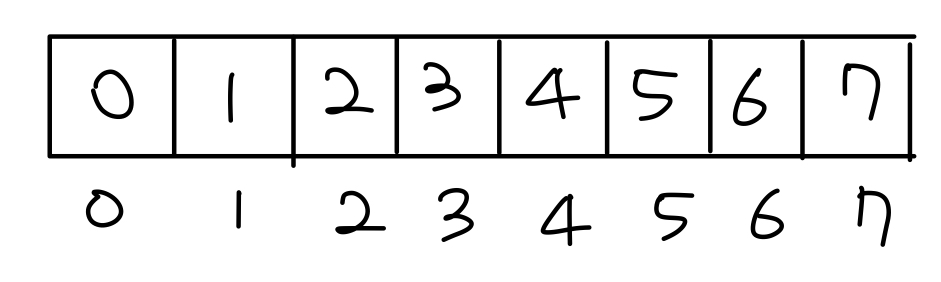
  • 초기 배열은 각 원소들이 자기 자신을 가리킨다. 즉, 모든 원소들은 분리되어 있는 상태이다.({0}, {1}, {2}, ...)
  • union 연산을 통해 하나둘씩 합쳐진다. ({0, 1}, {2}, {3, 5, 6}, ...)
  • 필요할 때 find 연산을 수행하여 특정 원소의 루트 노드가 무엇인지 알아낸다.


[배열 초기화]

1
2
3
4
5

int[] parent = new int[n];

for(int i=0; i<n; i++){
    parent[i] = i;
}

초기 배열


[초기 find 로직]

1
2
3
4
5
6

int find(int x){
    if (parent[x] == x){
        return x;
    }
    return find(parent[x]);
}
  • 루트 노드는 자기 자신을 가리킨다.
  • 따라서 find 연산은 루트 노드를 찾을 때까지 재귀적으로 탐색한다.


[find 성능 개선]

1
2
3
4
5
6

int find(int x){
    if (parent[x] == x){
        return x;
    }
    return parent[x] = find(parent[x]);
}
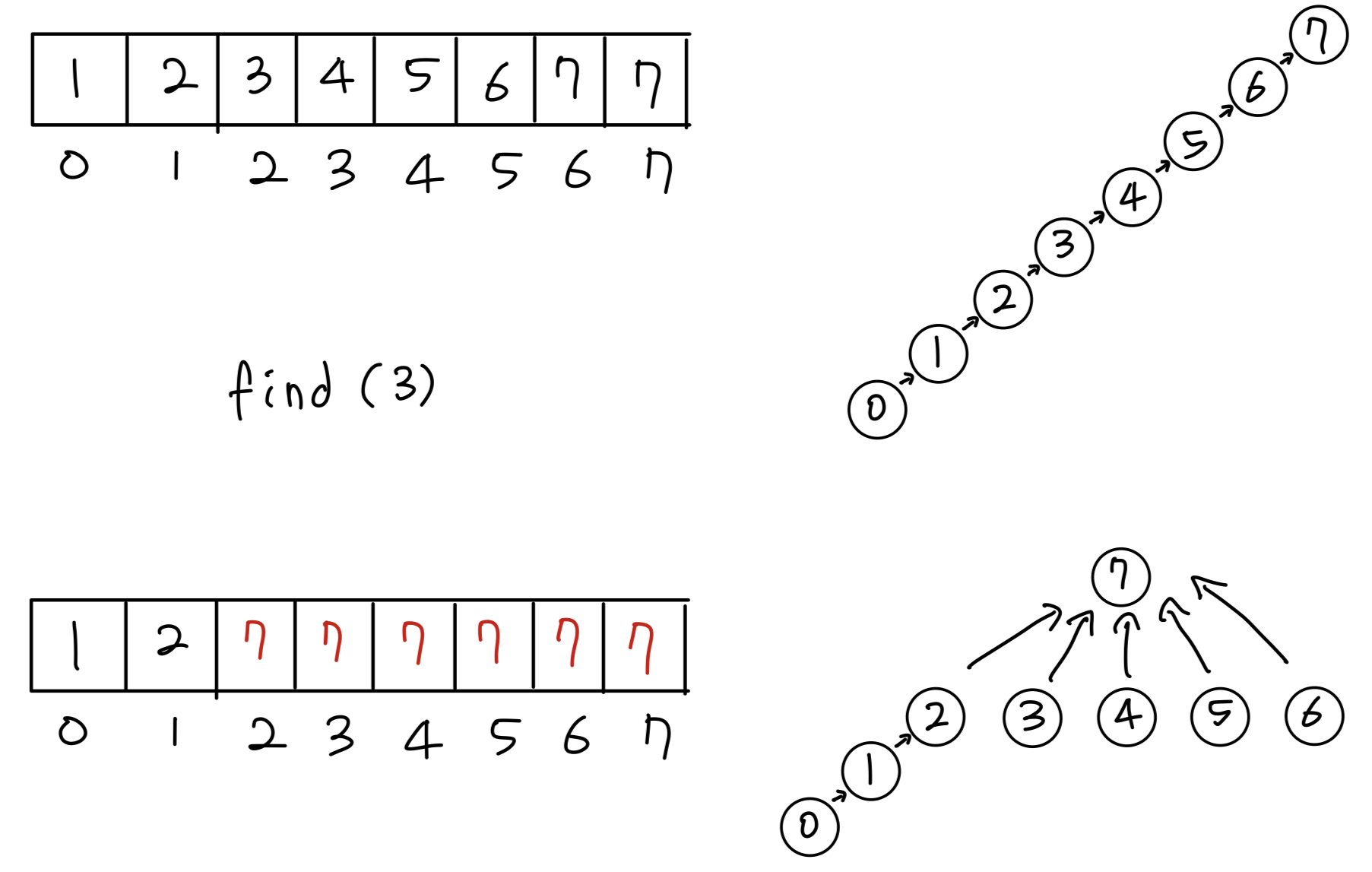
  • 그러나 한 방향으로 길게 뻗는 편중현상이 생길 수 있고 매번 긴 트리를 탐색하면 성능에 문제가 생긴다.
  • 따라서 위와 같이 한번 탐색하면 루트 노드를 저장하는 경로 압축 기법을 사용한다.

경로 압축

  • 경로 압축 기법을 통해 한번 탐색했던 원소의 find 연산의 시간 복잡도가 f(n)에서 f(1) 이 되었다.


[union 로직]

1
2
3
4
5
6
7
8
9
10

void union(int x, int y){
    int rootX = find(x);
    int rootY = find(y);

    if(rootX > rootY) {
        parent[rootY] = rootX;
    } else {
        parent[rootX] = rootY;
    }
}
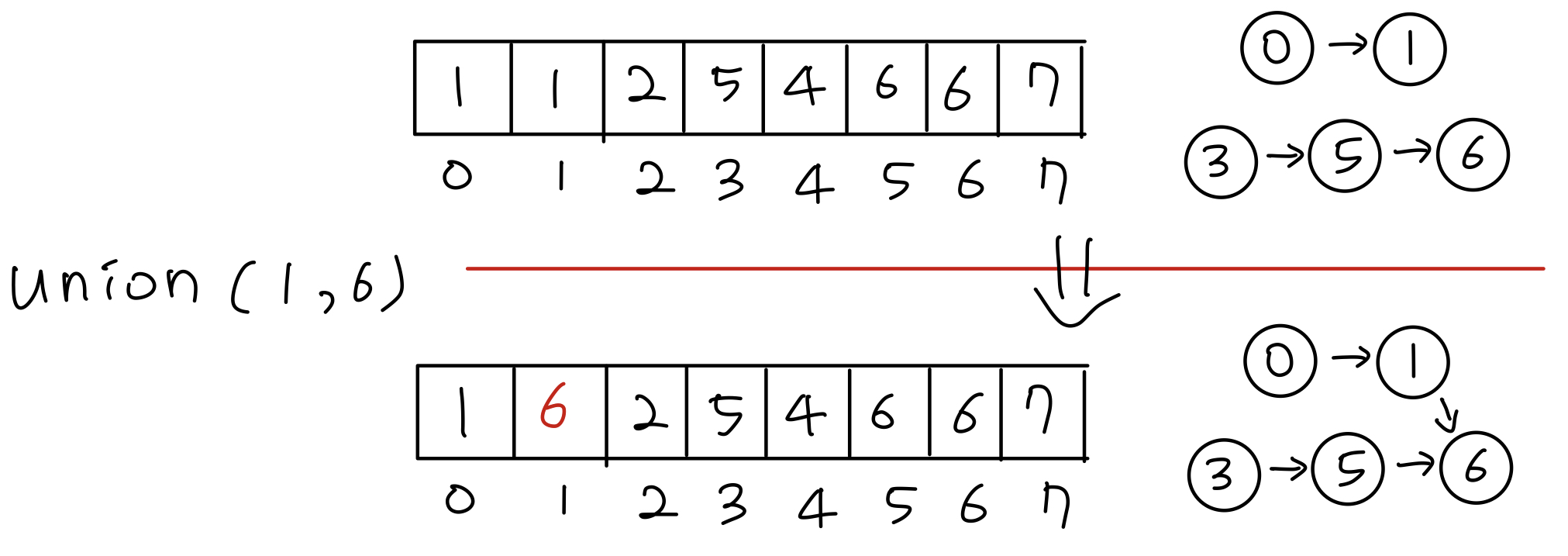
  • 기본적으로 순수한 유니온 파인드 알고리즘에서는 합칠 때의 기준이 인덱스가 더 큰쪽을 루트 노드로 설정하는 것이다.
  • 따라서 루트 노드의 대소비교를 통해 큰 쪽의 루트 노드가 합쳤을 때의 루트 노드가 되도록 설계한다.

union1

union2

BOJ 1717 - 집합의 표현 (골드 5)

1717-집합의 표현

  • 기본적인 유니온 파인드를 구현하는 문제이다.
  • union, find 함수를 구현한 후 각 줄 입력의 첫번째 정수에 따라 find 연산을 할지, union 연산을 할지를 분기해주면 된다.


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

import java.io.*;
import java.util.*;

public class Main {

    static FastReader scan = new FastReader();
    static StringBuilder sb = new StringBuilder();

    static int n;
    static int m;

    static int[] set;

    public static void main(String[] args) {
        input();
    }

    static void input() {
        n = scan.nextInt();
        m = scan.nextInt();

        set = new int[n+1];

        for (int i = 0; i < n + 1; i++) {
            set[i] = i;
        }

        for (int i = 0; i < m; i++) {
            solve(scan.nextLine());
        }
    }

    static void solve(String s) {
        StringTokenizer sst = new StringTokenizer(s);

        int menu = Integer.parseInt(sst.nextToken());
        int a = Integer.parseInt(sst.nextToken());
        int b = Integer.parseInt(sst.nextToken());

        if (menu == 0) {
            union(a, b);
        } else {
            if (find(a) == find(b)) {
                System.out.println("yes");
            } else {
                System.out.println("no");
            }
        }
    }

    static int find(int x) {
        if (set[x] == x) {
            return x;
        }
        return set[x] = find(set[x]);
    }

    static void union(int x, int y) {
        int parentx = find(x);
        int parenty = find(y);

        if (parentx > parenty) {
            set[parenty] = parentx;
        } else {
            set[parentx] = parenty;
        }
    }

    static class FastReader {
        .
        .
        .
    }
}


유니온 파인드를 사용하는 문제 리스트

간단한 개념 하나를 아는 것만으로도 골드 난이도의 문제들을 풀 수 있다는 것이 정말 꿀문제인 것 같다.


누군가가 물어본다면

유니온 파인드는 두 원소가 같은 집합에 속하는지를 알고자 하는 문제에 사용할 수 있는 기법입니다.
algorithm
algorithm BOJ union-find 유니온 파인드
This post is licensed under CC BY 4.0 by the author.